Um tubo de drenagem circular, de concreto sem acabamento, é assentado em um declive de 0,0025 e está planejado para conduzir de 1,4 a 8,5 m3/s de água drenada. As restrições do projeto são que (1) a profundidade da água não pode ultrapassar 3/4 do diâmetro e (2) o escoamento deve ser sempre subcrítico. Qual é o diâmetro apropriado para satisfazer a esses requisitos? Se não houvesse nenhum tubo comercial com esse diâmetro exato, você compraria o tubo do diâmetro mais próximo menor ou maior?

Pra começo de conversa, temos que descobrir qual o ângulo pra esse caso específico. Bem, por simples análise trigonométrica, se a altura não pode passar do diâmetro, .

Sendo assim, podemos calcular e .

Pra calcular a vazão necessária pra mante esse escoamento, utilizamos a equação 10.19, apresentada na página 714:

Vamos considerar, então, , a vazão volumétrica máxima que o escoamento assumirá. Se essa vazão cumprir os requisitos, as outras também irão.

Sendo assim:

Logo, .

Agora, devemos checar se o escoamento é subcrítico. Pra isso, basta a gente olhar pra esse esquema do tubo:

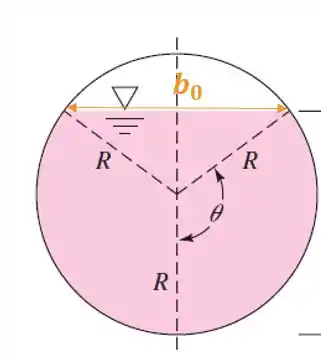
Podemos descobrir o tamanho da largura pro caso do nosso tubo, devemos utilizar simples propriedades trigonométricas:

Podemos também calcular a vazão crítica a partir da equação 10.37a, dada na página 721:

Utilizando novamente algumas propriedades trigonométricas simples:

Como o escoamento é subcrítico, e cumprimos um dos objetivos.

Agora, pra finalizar a questão, vamos responder à pergunta no fim do enunciado: a gente escolheria um diâmetro próximo maior ou menor que o calculado?

Bem, como o escoamento será subcrítico mesmos e aumentarmos o diâmetro, pois como vimos no passo anterior a vazão crítica vai ser maior se a área for maior, então vamos escolher o diâmetro um pouco acima.

Pronto, matamos a questão juntos!