Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 122

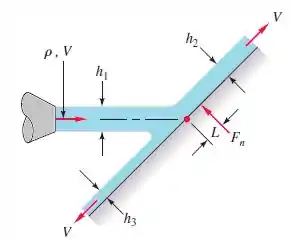
Estenda o problema P3.46 para o problema de calcular o centro de pressão L da força normal F n , como mostra na figura abaixo. (No centro de pressão, não são necessários momentos para manter a placa em repouso.) Despreze o atrito. Expresse seu resultado em termos da espessura h 1 da camada e do ângulo θ entre a placa e o jato de entrada.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)

Relembrando lá do problema 3.46, a gente encontrou que h 2 = ( h 1 2 ) ( 1 + c o s θ ) e que h 3 = ( h 1 2 ) ( 1 - c o s θ ) .

Vamos dar nome aos ângulos do nosso problema atual!!

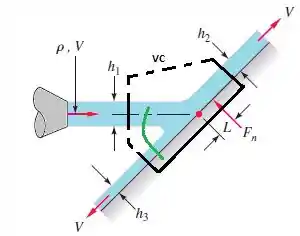
Nosso ângulo θ será representado pela linha verde no desenho de cima!!

Passo 2

A força que atua na placa era F n = ρ Q V s e n θ . Vamos agora tomar o momento em torno da origem do meu desenho aí de cima, representado pela bolinha rosinha no centro da placa, temos que:

∑ M o = - F n L = m ˙ 2 r 2 o × V 2 z + m ˙ 3 r 3 o × V 3 z - m ˙ 1 r 1 o × V 1 z

∑ M o = ρ V h 2 h 2 V 2 + ρ V h 3 - h 3 V 2 - 0 = 1 2 ρ V 2 h 2 2 - h 3 2

Passo 3

Portanto temos também que:

L = - 1 2 ρ V 2 h 2 2 - h 3 2 ρ V 2 h 1 s e n θ = - h 2 2 - h 3 2 2 h 1 s e n θ = - 1 2 h 1 c o t θ

O último resultado segue da relação ( h 1 ,   h 2 ,   h 3 ) do problema 3.46. O centro de pressão é ABAIXO do ponto de origem!!!

Resposta

L = - 1 2 h 1 c o t θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere dois corpos rígidos com mesma massa e velocidade angular. Você acha que esses dois corpos devem ter o mesmo momento angular? Explique.
Descreva as forças de corpo e as forças de superfície e explique como a força resultante que age sobre o volume de controle é determinada. O peso do fluido é uma força de corpo ou uma força de superfí
Em determinado local, um helicóptero exige mais energia no verão ou no inverno para atingir um desempenho especificado? Explique.
Para flutuar no alto de uma montanha, um helicóptero precisa de mais, menos ou da mesma potência que precisaria para flutuar no nível do mar? Explique.
Um jato d’água horizontal de um bocal com seção transversal de saída constante atinge normalmente uma placa plana vertical e fixa. Determinada força F é necessária para manter a placa contra a corrent