Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 7
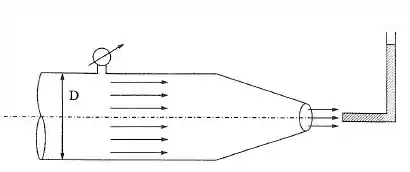
Na extremidade de uma tubulação de diâmetro , acha-se instalado um bocal que lança um jato de água na atmosfera com diâmetro de . O manômetro metálico registra uma pressão de e a água sobe no tubo de Pitot até a altura de . Nessas condições, determinar:
- A vazão em peso do escoamento;
- O diâmetro do tubo, admitindo escoamento permanente e sem atrito.
.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos identificar cada ponto que é interessante ser estudado. Vamos chamar de ponto , o ponto na saída da tubulação e de ponto , o ponto na entrada do tubo de Pitot.
Aplicando Bernoulli, temos que:
As cotas são iguais:
Temos a carga de pressão no ponto .
A velocidade no ponto é nula pois está no chamado ponto de estagnação e a pressão relativa no ponto é nula pois está ao ar livre, logo:
Substituindo os pontos, temos que:
Passo 2
Podemos então encontrar a vazão mássica no ponto :
Portanto:
A vazão em peso será:
Passo 3
Para descobrir o diâmetro , vamos chamar de ponto o ponto abaixo do manômetro. Sabemos que no ponto teremos carga cinética e de pressão e no ponto somente carga cinética. Portanto:
Resolvendo, temos que:
Aplicando a equação da continuidade, temos que:
Substituindo, temos que:
Resolvendo, temos que: