Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 21

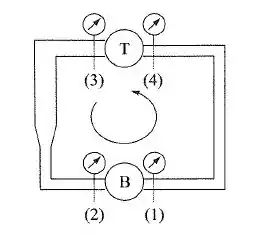
No circuito da figura instalado num plano horizontal, tem-se p 1 = 0,3   M P a ; p 2 = 0 ; p 3 = 0,1   M P a ; N T = 6   k W ; η T = 0,75 ; A 1 = A 2 = A 4 = 80   c m 2 ; A 3 = 100   c m 2 ; γ = 10 4   N / m 3 .

A potência que o fluido recebe da bomba é o dobro da potência da turbina. Determinar:

a) a vazão;

b) a perda de carga no trecho da direita;

c) a leitura do manômetro (4);

d) a perda de carga no trecho da esquerda.

Passo 1

Vamos começar o exercício aplicando o equilíbrio de cargas entre os pontos 1 e 2:

H 1 = H 2 + H B

Abrindo a expressão:

v 1 2 2 g + p 1 γ + z 1 = v 2 2 2 g + p 2 γ + z 2 + H B

Isolando H B e substituindo os valores conhecidos (sabendo que a velocidade é a mesma para 1 e 2 já que os tubos possuem a mesma área de seção transversal e que z 1 = z 2 já que os pontos estão no mesmo nível:):

H B = v 1 2 2 g + p 1 γ + z 1 - v 2 2 2 g + p 2 γ + z 2

H B = p 1 γ - p 2 γ = 0,3.10 6 10 4 - 0 10 4 → H B = 30   m

Agora, usando a informação dada no enunciado de que a potência que o fluido recebe da bomba é o dobro da potência da turbina, podemos escrever:

γ Q H B = 2 η T γ Q H T

Simplificando a expressão e isolando H T :

H T = H B 2 η T = 30 2 0,75 → H T = 20   m

Agora, através da equação da potência da bomba, temos:

N T = η T γ Q H T → Q = N T η T γ H T = 6.10 3 0,75 ( 10 4 ) ( 20 ) → Q = 0,04   m 3 / s

Passo 2

Agora vamos resolver a letra b). Vamos começar encontrando as velocidades nos pontos 2 e 3 através da equação da vazão:

v 2 = Q A 2 = 0,04 80.10 - 4 → v 2 = 5   m / s

v 3 = Q A 3 = 0,04 100.10 - 4 → v 3 = 4   m / s

Agora vamos aplicar o equilíbrio de cargas entre os pontos 2 e 3:

H 2 + H B - H T = H 3 + H p 1,4

Agora abrindo a expressão:

v 2 2 2 g + p 2 γ + z 2 + H B - H T = v 3 2 2 g + p 3 γ + z 3 + H p 1,4

Isolando H p 1,4 e substituindo os valores conhecidos (lembrando que z 2 e z 3 estão no mesmo nível):

H p 1,4 = v 2 2 2 g + p 2 γ + z 2 + H B - H T - v 3 2 2 g + p 3 γ + z 3

H p 1,4 = 5 2 2 ( 10 ) + 0 10 4 + 30 - 20 - 4 2 2 10 + 0,1.10 6 10 4 → H p 1,4 = 0,45   m

Passo 3

Agora, para resolver a letra c), vamos aplicar o equilíbrio de cargas entre os pontos 1 e 4:

H 1 = H 4 + H p 1,4

Abrindo a expressão, temos:

p 1 γ + v 1 2 2 g + z 1 = p 4 γ + v 4 2 2 g + z 4 + H p 1,4

Isolando p 4 e susbtituindo os valores conhecidos (sabendo que 1 e 4 estão no mesmo nível e que possuem as mesmas áreas de seção transversal, logo, têm as mesmas velocidades):

p 4 = γ p 1 γ + v 1 2 2 g + z 1 - v 4 2 2 g + z 4 + H p 1,4

p 4 = 10 4 0,3.10 6 10 4 - 0,45 → p 4 = 295,5   k P a

Passo 4

Agora para resolver a letra d), vamos aplicar o equilíbrio de cargas entre os pontos 2 e 3:

H 3 = H 2 + H p 3,2

Abrindo a expressão:

p 3 γ + v 3 2 2 g + z 3 = p 2 γ + v 2 2 2 g + z 2 + H p 3,2

Isolando H p 3,2 e substituindo os valores conhecidos (sabendo que 2 e 3 estão no mesmo nível):

H p 3,2 = p 3 γ + v 3 2 2 g + z 3 - p 2 γ + v 2 2 2 g + z 2

H p 3,2 = 0,1.10 6 10 4 + 4 2 2 ( 10 ) - 0 10 4 + 5 2 2 10 → H p 3,2 = 9,55   m

Resposta

Q = 0,04   m 3 / s

H p 1,4 = 0,45   m

p 4 = 295,5   k P a

H p 3,2 = 9,55   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um escoamento em regime permanente, incompressível e sem atrito sobre a asa de um aeroplano voando a 200 km/h. O ar que se aproxima da asa está a 65 kPa (manométrica) e -10°C. Em certo ponto
Uma corrente de líquido movendo a baixa velocidade sai de um bocal apontado diretamente para baixo. A velocidade pode ser considerada uniforme na seção de saída do bocal e os efeitos de atrito podem s
Água escoa de um tanque muito grande através de um tubo de 5 cm de diâmetro. O líquido escuro no manômetro é mercúrio. Estime a velocidade no tubo e a vazão de descarga. (Considere o escoamento sem at
Um barômetro de mercúrio é transportado em um carro em um dia em que não há vento e a temperatura do ar é 20°C. A leitura correta do barômetro é 761 mm de mercúrio. Uma janela é ligeiramente aberta qu
Uma lata de refrigerante (você não sabe se a bebida é diet ou normal) possui um pequeno vazamento em um orifício, que pulveriza o refrigerante verticalmente para cima no ar a uma altura de 0,5 m. Qual