Exercícios de Equação da Energia e Bernoulli - Lista de Exercícios Resolvida
Questão 1
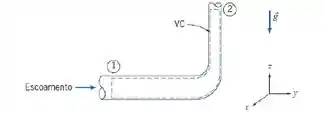
(Adaptada) Medidas foram feitas para a configuração de escoamento de água mostrada na figura. Na entrada, seção 1, a pressão é 70kPa (manométrica), a velocidade média é 1,75 m/s e a elevação é 2,25 m. Na saída, seção 2, a pressão, a velocidade média e a elevação são, respectivamente, 45 kPa (manométrica), 3,5 m/s e 3 m, respectivamente. Calcule a perda de carga em metros.
Questão 2
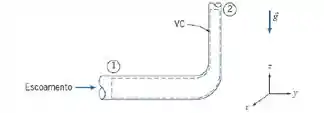
Para a configuração de escoamento da figura, é sabido que a perda de carga é 1 m. Da entrada para a saída, a queda de pressão é 50 kPa, a velocidade dobra da entrada para a saída, e o aumento de elevação é de 2 m. Calcule a velocidade de entrada da água.
Questão 3
(Adaptada) Água escoa em um tubo horizontal de área transversal constante; o diâmetro do tubo é 75 mm e a velocidade média do escoamento é 5 m/s. Na entrada do tubo, a pressão manométrica é 275 kPa e a saída é à pressão atmosférica. Determine a perda de carga no tubo.
Ver solução completaQuestão 4
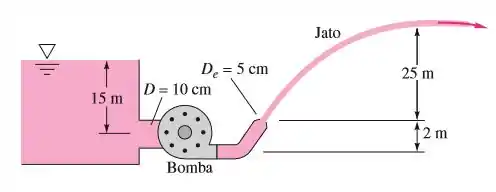
A bomba da figura abaixo cria um jato d’água a , orientado para atingir uma distância horizontal máxima. As perdas por atrito do sistema são de . O jato pode ser aproximado pela trajetória de partículas sem atrito. Que potência a bomba deve entregar à água?
Questão 5
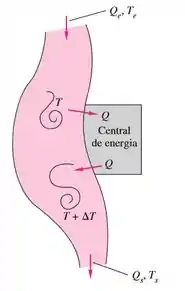
Uma central de energia às margens de um rio, como na figura abaixo, deve eliminar de calor perdido para o rio. As condições do rio a montante são e . O rio tem de largura e de profundidade. Se as perdas de calor para a atmosfera e para o solo são desprezíveis, calcule as condições do rio a jusante .
Questão 6
Quando a bomba da figura abaixo bombeia de água a do reservatório, a perda de carga total por atrito é de . O escoamento descarrega através de um bocal para a atmosfera. Calcule a potência da bomba em entregue para a água.
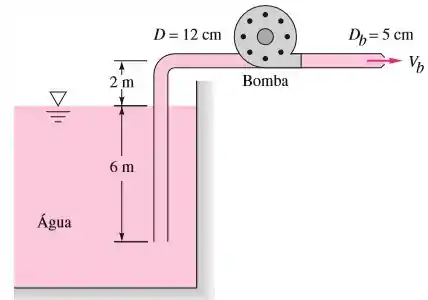
Questão 7
Considere a turbina extraindo energia através de um conduto forçado em uma barragem, como na figura abaixo. Para escoamento turbulento em dutos, a perda de carga por atrito é aproximadamente , em que a constante depende das dimensões do conduto forçado e das propriedades da água. Mostre que, para uma dada geometria de conduto forçado e vazão variável do rio, a máxima potência possível da turbina nesse caso é e ocorre quando a vazão é .
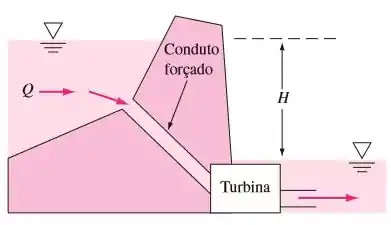
Questão 8
Um jato de álcool atinge a placa vertical da figura abaixo. Uma força é necessária para manter a placa estacionária. Considerando que não há perdas no bocal, calcule o fluxo de massa de álcool e a pressão absoluta na seção .
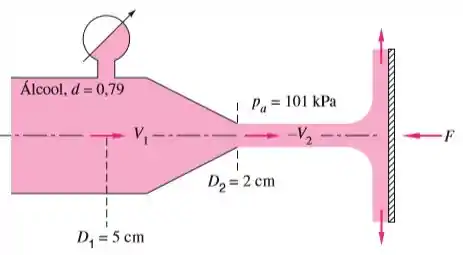
Questão 9
Dois reservatórias de água abertos para a atmosfera são conectados por uma tubulação de mesmo material e diâmetro constante de 50 mm e uma máquina hidráulica M, garantindo-se um escoamento permanente, conforme esquematizado na figura abaixo. Os seguintes dados são fornecidos para essa instalação: , , , , , e . Pede-se:
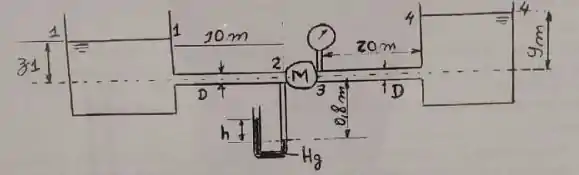
- Calcular a perda de carga entre as seções 3 e 4, ou 4 e 3
Questão 10
Em um sistema de movimentação de ar apresentado na figura há entrada de ar pela seção 1-1, seguida de um trocador de calor que pode aquecer o ar (condição A) ou não aquecer (condição B). Em seguida o ar é inserido em uma caixa de distribuição de ar podendo escoar para três saídas nas seções 3-3, 4-4 e 6-6. Na seção 5-5 há um pistão que pode movimentar-se ou estar travado em repouso. Na seção 6-6 há um tubo de Pitot posicionado de modo a medir uma velocidade que tem um valor muito próximo ao valor da velocidade média nesta seção transversal, seguido por um ventilador auxiliar.
São dados:
- Na seção 1-1: Vazão em massa , massa específica e área
- Na condição A o trocador de calor aquece o ar e sua massa específica na seção 2-2 é
- As áreas das seções de saída são: e
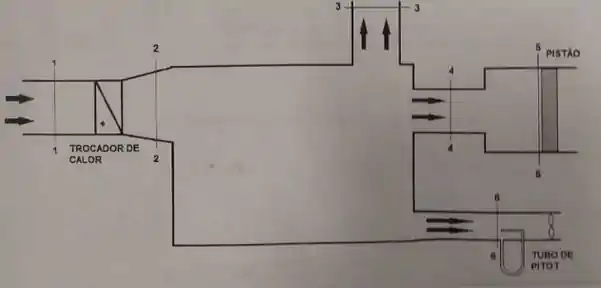
Pede-se:
- Desenvolver uma expressão para calcular a velocidade medida com o tubo de Pitot a partir da equação de Bernoulli aplicada na seção 6-6, na qual são medidas as pressões estática e total. Considerando a mesma condição do item 1.1, calcular o valor da pressão dinâmica medida por este instrumento (pdin)
Questão 11
Óleo SAE 10 a 20°C , escoa no interior do tubo vertical liso de 30 mm de diâmetro interno mostrado na figura. O desnível do manômetro de mercúrio é de 420 mm, conforme mostrado na figura. A aceleração da gravidade é de 9,8 m/s². Determine:
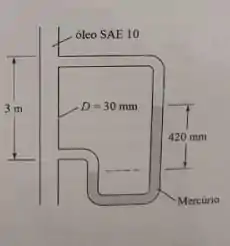
- O sentindo do escoamento
Questão 12
Um bocal foi projetado para acelerar o escoamento de um fluido da velocidade na entrada V1 para velocidade V2 na saída de modo linear. Assim a velocidade pode ser expressa por com a e b constantes. Pedem-se:
2.2. Adote agora uma nova hipótese de que o escoamento é transitório. Nestas condições considere que , e que no instante em que V1 = 10 m/s, e em que V2 = 25 m/s. Determine novamente as acelerações locais, convectiva e total nos pontos x1 e x2
Ver solução completaQuestão 13
Dois reservatórias de água abertos para a atmosfera são conectados por uma tubulação de mesmo material e diâmetro constante de 50 mm e uma máquina hidráulica M, garantindo-se um escoamento permanente, conforme esquematizado na figura abaixo. Os seguintes dados são fornecidos para essa instalação: , , , , , e . Pede-se:
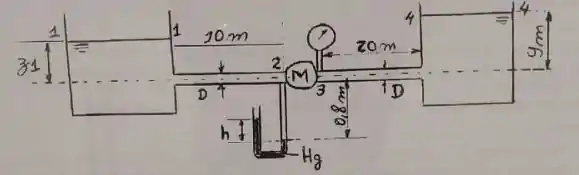
- Mostrar por meio de cálculo o sentido do escoamento. Justificar o valor do coeficiente de energia cinética adotado
Questão 14
Dois reservatórias de água abertos para a atmosfera são conectados por uma tubulação de mesmo material e diâmetro constante de 50 mm e uma máquina hidráulica M, garantindo-se um escoamento permanente, conforme esquematizado na figura abaixo. Os seguintes dados são fornecidos para essa instalação: , , , , , e . Pede-se:
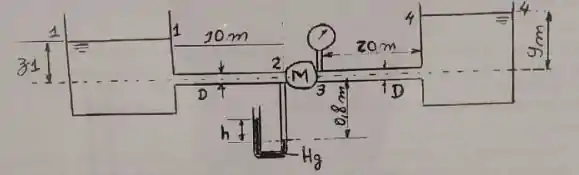
- Calcular a potência hidráulica trocada pela máquina com o fluido, em watts.
Questão 15
Um bocal foi projetado para acelerar o escoamento de um fluido da velocidade na entrada V1 para velocidade V2 na saída de modo linear. Assim a velocidade pode ser expressa por com a e b constantes. Pedem-se:
2.1 Admitindo que o regime é permanente e que a velocidade V1 = 10 m/s com , e que a velocidade em , determinar as acelerações local, convectiva e total nos pontos e
Ver solução completa