Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 16

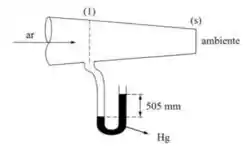
Na figura, o ar apresenta escoamento isentrópico, bloqueado. Sabendo que a pressão de estagnação é 2 ⋅ 10 5   P a   ( a b s ) , determinar A 1 . Dados: k = 1,4 ; R = 287   m 2 / s 2 K ; A s = 15   c m 2 ; p a t m = 10 5   P a ;   γ H g = 136000   N / m 3

Passo 1

Dados da questão:

  • Pressão de estagnação: p 0 = 2 ⋅ 10 5   P a   ( a b s )
  • Constante isentrópica: k = 1,4
  • Constante do gás: R = 287   m 2 / s 2 K
  • Área de saída: A s = 15   c m 2
  • Pressão atmosférica: p a t m = 10 5   P a
  • Peso específico: γ H g = 136000   N / m 3

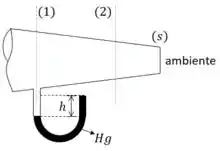
Para resolver essa questão podemos utilizar a Tabela 1. Vamos calcular a pressão no ponto 1 e usar a relação com a pressão de estagnação para calcular a área:

Passo 2

Inicialmente vamos calcular a pressão no ponto 1, com base no manômetro de mercúrio:

p 1 - γ H g h = p a t m

p 1 = p a t m + γ H g h

Aplicando os valores:

p 1 = 10 5   P a + 136000   N / m 3 ⋅ 0,505   m  

p 1 = 168,68   k P a   ( a b s )  

Passo 3

Vamos calcular a relação de entre as pressões:

p 1 p 0 = 168680 200000 = 0,8434

Agora, podemos pegar a relação entre as áreas na Tabela 1 no fim do livro:

A 1 A * = 1,340

Isolando A 1

A 1 = 1,34 A *

Aplicando os valores:

A 1 = 1,34 ⋅ 15   c m

A 1 = 20,1   c m 2

Resposta

A 1 = 20,1   c m

Ver Outros Exercícios desse livro