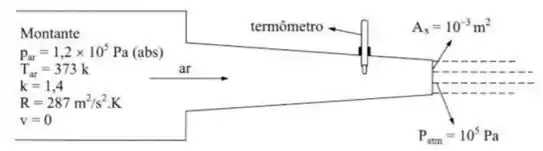
O reservatório de grandes dimensões da figura descarrega o ar à atmosfera com escoamento isentrópico.

1. Qual é a temperatura indicada no termômetro?
2. Qual é a vazão em massa na seção de saída?
3. Qual é a vazão em massa na seção onde ?
4. Qual é a área da seção onde
5. Qual é a máxima vazão em massa que poderia ser obtida e como poderia ser provocada sem alterar a leitura do termômetro?

Para calcular a vazão na saída podemos usar a fórmula:

Já temos o valor da área de saída! Para calcular a velocidade precisaremos do número de Mach e da Temperatura. Para calcular a densidade podemos usar a equação dos gases, e pra isso precisaremos da temperatura. Podemos encontrar esses valores na Tabela 1 (no fim do livro).

Primeiro calculamos a relação de pressão:

Observando a Tabela 1 podemos extrair o número de Mach e a razão entre temperaturas. Para evitar interpolações, vamos usar os valores selecionados:

Podemos determinar a temperatura na saída:

Agora, vamos usar a equação dos gases para determinar a densidade:

E podemos calcular a velocidade:

E agora podemos calcular a vazão mássica:

Agora a pergunta é: Qual é a vazão em massa na seção onde ?

Bem, a verdade é que não haverá mudanças na vazão mássica, uma vez que este é um regime permanece subsônico.

Para calcular a área da seção, vamos usar uma variação da fórmula da vazão:

Pela tabela 1, quando o número de Mach é igual a :

Pela tabela podemos determinar pressão e temperatura:

Agora, vamos usar a equação dos gases para determinar a densidade:

E podemos calcular a velocidade:

Finalizamos calculando a área:

A máxima vazão obtida com a mesma temperatura é quando o regime esta em situação crítica

Pela tabela 1, quando o número de Mach é igual a :

Pela tabela podemos determinar pressão crítica e temperatura na saída:

Agora, vamos usar a equação dos gases para determinar a densidade na saída:

E podemos calcular a velocidade na saída:

Finalizamos calculando a área: