Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 23
A figura mostra um bocal convergente/divergente, em que o escoamento é isentrópico, bloqueado e contínuo. O reservatório a montante é de grandes dimensões.
- Determinar a pressão, a temperatura e a massa específica da estagnação
- Determinar a pressão e a temperatura na garganta do bocal
- Se o tubo de Pitot for instalado na seção (2), qual será o novo desnível do mercúrio, mantido o outro ramo do manômetro diferencial? (Justifique)
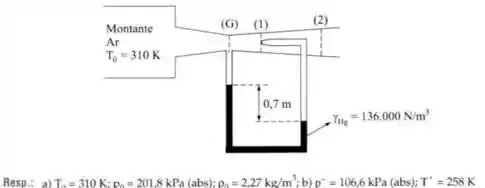
Passo 1
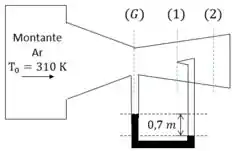
Já possuímos a temperatura de estagnação
Pela diferença de altura de mercúrio podemos relacionar a pressão no ponto G à pressão de estagnação:
Mas para aplicar essa equação precisaremos da pressão em (G). Sabemos que o ponto é a garganta do fluxo, ou seja, neste ponto o número de Mach é igual a um:
A tabela 1 nos fornece uma relação entre a pressão em G e a pressão de estagnação
Agora podemos determinar a pressão de estagnação:
Para encontrar a densidade do ar basta aplicar a equação dos gases ideais:
Passo 2
Agora, utilizando a tabela 1, podemos determinar as propriedades do ponto G:
Passo 3
Independentemente de onde esteja instalado, o tubo de Pitot irá medir a pressão de estagnação. Então, se o manômetro continuar conectado ao ponto G não haverá mudança na altura do mercúrio.
Resposta
- Não há mudança na coluna de mercúrio