Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 164
Na Figura P3.164, o jato aberto de água a 20°C sai de um bocal para o ar ao nível do mar e atinge um tubo de estagnação, como mostra a figura. Se a pressão na linha de centro na seção 1 é 110 kPa e as perdas são desprezadas, calcule (a) o fluxo de massa em kg/s e (b) a altura H do fluido no tubo de estagnação.
Passo 1
Vamos começar encontrando o fluxo mássico de água que sai pelo bocal, para isso utilizaremos a igualdade:
Neste caso, e Q é dada por:
Onde é a área da seção transversal do bocal:
Agora só resta encontrarmos .
Passo 2
Para encontrarmos a velocidade da água que sai pelo bocal teremos que utilizar Bernoulli:
Neste caso iremos considerar um ponto em 1 (ponto 1) e um ponto na saída do bocal (ponto 2), os dois estão na mesma altura () e a pressão em 2 é a atmosférica ().
Podemos escrever, pela equação da continuidade, que:
Agora é só substituir:
Passo 3
Agora que temos a velocidade de saída do fluido é só achar a vazão volumétrica e em seguida a vazão mássica:
Passo 4
Para calcular a altura H do fluido na coluna de estagnação é só utilizar a equação de Bernoulli nos seguintes pontos:
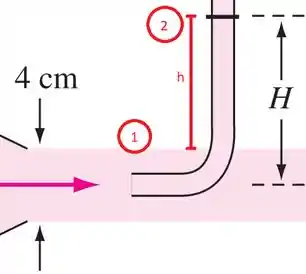
Vamos fazer desta maneira, pois nestes pontos as pressões são iguais, ou seja, e no ponto 2 a velocidade é zero () já que é um tubo de estagnação. Vamos considerar que .
Aplicando Bernoulli entre os dois pontos:
Encontramos a altura entre os dois pontos (h), porém o exercício pede o valor de H que pode ser escrito como a soma de h e metade do diâmetro do jato de saída, ou seja:
Resposta
Letra a)
Letra b) .