Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas para exames de fundamentos de engenharia - Ex. 8
A bomba de um barco anti-incêndio fornece água para um bocal vertical com uma relação de diâmetro 3:1, como na Figura FE3.6. Se o atrito no duto e no bocal é desprezado e a bomba fornece 3,75 m de altura ao escoamento, qual será a vazão volumétrica na saída?
(a)322 L/min, (b) 454 L/min, (c) 583 L/min, (d) 821 L/ min, (e) 1.079 L/min.
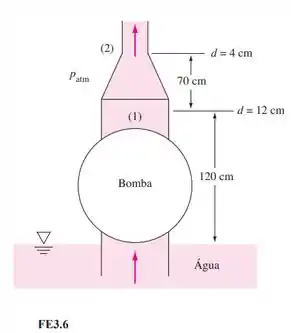
Passo 1
Vamos utilizar a equação de Bernoulli entre um ponto na superfície (ponto 0) e o ponto 2:
Vamos utilizar o ponto 0 como referencial para a altura, logo, . As pressões em 0 e 2 são ambas iguais a atmosférica e a velocidade em 0 é aproximadamente zero.
Aplicando os dados em Bernoulli:
A área da seção transversal do tubo em 2 é:
E a vazão pode ser encontrada por:
Resposta
Letra B) (b) 454 L/min
Exercícios de Livros Relacionados
A forma incompressível da equação de Bernoulli, Equação (3.77), é precisa apenas para escoamentos com números de Mach menores que 0,3, aproximadamente. Para velocidades mais altas, a variação de densi
O líquido incompressível no grande tanque da Figura P3.180 está em repouso quando, em t = 0 , a válvula é aberta para a atmosfera. Admitindo h ≈ c o n s t a n t e (velocidades e acelerações desprezíve
O escoamento de água a 35°C da Figura P3.172 descarrega para a atmosfera padrão ao nível do mar. Desprezando as perdas, para qual diâmetro D do bocal começa a ocorrer cavitação? Para evitar a cavitaçã
Modifique o Problema P3.180 como se segue. Considere o topo do tanque fechado e sob uma pressão manométrica constante p 0 . Repita a análise e encontre V(t) no tubo.
Se a velocidade de aproximação não for alta demais, uma saliência no fundo de um canal d’água causará um afundamento ∆ h do nível da água, que pode servir para medição de vazão. Se, como mostra a Figu