Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 60

Um fluido quente passa através de um tubo de parede delgada, com 10   m m de diâmetro e 1   m de comprimento, e um refrigerante a T ∞   =   25 ° C escoa em escoamento cruzado sobre o tubo. Quando a vazão é m = 18   k g / h e a temperatura na entrada é T m , e n t =   85 ° C , a temperatura na saída é T m , s a i   =   78 ° C .

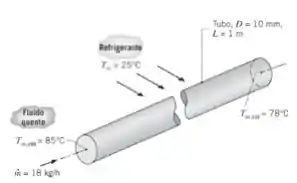
Admitindo o escoamento e as condições térmicas no interior do tubo plenamente desenvolvidas, determine a temperatura de saída, T m , s a i , se a vazão for duplicada. Isto é, m =   36   k g / h , com todas as demais condições inalteradas. As propriedades termofísicas do fluido quente são: ρ = 1079   k g / m 3 , c p = 2637   J / ( k g ⋅ K ) , μ = 0,0034   N · s / m 2 e k   =   0,261   W / ( m   ·   K ) .

Passo 1

Beleza galerinha, vamos lá! Nesta questão, vamos calcular a temperatura de saída, considerando que o fluxo aumenta. Legal né? (Vai... é legal sim 😊!) Para as condições prescritas no esquema, a equação 8.45a pode ser usado para avaliar o coeficiente global de convecção com P = π D ,

T ∞ - T m , o T ∞ - T m , i = exp ⁡ - P L m o c p U

Do esquema da questão,

25 - 78 ° C 25 - 85 ° C = exp ⁡ - π × 0.01 m × 1 m ( 18 / 3600 )   k g / s × 2637   J / k g   ⋅ K U

Isolando,

U = 52.1   W / m 2 ⋅ K

Passo 2

Tá galera, pra que a gente achou o coeficiente global? Porque ele pode ser expresso em termos de coeficientes internos e externos, que é o que a gente quer de verdade. Temos então que:

U = 1 h 1 + 1 h o - 1

Caracterizamos o fluxo interno com o Número de Reynolds, temos:

R e D = 4 m π D μ = 4 × 18 3600 k g / s π × 0.01 m × 0.0034 N ⋅ s / m 2 = 187

Passo 3

E olha que legal, para esse valor do número de Reynolds, caracterizamos esse fluxo como laminar. Ou seja, o h i não vai mudar quando a taxa é duplicada. Ou seja, o nosso U não muda quando o m = 2 m . Portanto, puxamos a nossa equação novamente para calcularmos a nova temperatura de saída,

25 - T m , o ° C 25 - 85 ° C = exp ⁡ - π × 0.01 m × 1 m ( 18 / 3600 )   k g / s × 2637   J / k g   ⋅ K 52.1   W / m 2 ⋅ K

Isolando a temperatura,

T m , o = 81.4   ° C

Resposta

T m , o = 81.4   ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um prestador de serviços na área de aquecimento deve aquecer 0,2 kg/s de água de 15°C até 35°C usando gases quentes em escoamento cruzado sobre um tubo de parede delgada.Sua tarefa é desenvolver uma s
Em um processo de fabricação de suprimentos biomédicos, há a exigência de que uma grande placa deva ser mantida a uma temperatura de 45 ± 0,25°C. O projeto proposto apresenta a fixação de tubos de aqu
Para uma entrada com arestas vivas e uma região de entrada combinada, o número de Nusselt médio pode ser calculado pela Equação 8.63, com C=24 R e D - 0.23 e m=0,815–2,08×10 – 6R e D[ 23 ] . Determine
Considere a bomba de calor do Problema 5.100, que usa o subsolo, em condições de inverno nas quais o líquido é descarregado pela bomba de calor no interior de um tubo de polietileno de alta densidade,
Água, a 290 K e 0,2 kg/s, escoa através de um tubo de Teflon (k = 0,35 W/(m · K)) com raios interno e externo iguais a 10 e 13 mm, respectivamente. Um fino aquecedor elétrico em forma de fita, enrolad