Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 77
Considere a bomba de calor do Problema 5.100, que usa o subsolo, em condições de inverno nas quais o líquido é descarregado pela bomba de calor no interior de um tubo de polietileno de alta densidade, com espessura t = 8 mm e condutividade térmica k = 0,47 W/(m · K). O tubo atravessa o solo, que mantém uma temperatura uniforme, de aproximadamente 10°C, na sua superfície externa. As propriedades do fluido podem ser aproximadas pelas da água.
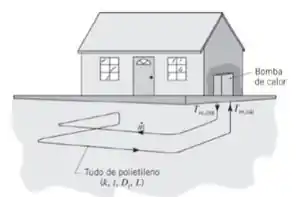
(a) Para um diâmetro interno do tubo e uma vazão de Di = 25 mm e = 0,03 kg/s, e uma temperatura na entrada do fluido de Tm,ent = 0°C, determine a temperatura do fluido na saída do tubo (temperatura na entrada da bomba de calor), Tm,sai, em função do comprimento do tubo L para 10 ≤ L ≤ 50 m.
(b) Recomende um comprimento apropriado para o sistema. Como sua recomendação seria afetada por variações na vazão do escoamento do líquido?
Passo 1
Beleza galerinha, vamos lá! (a) Para as condições prescritas, o fluxo é laminar. Portanto, utilizando a eq. 8.57, temos:
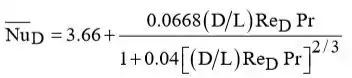
Com Ts usado no lugar de T∞, Eq. 8.45b pode ser usado para determinar Tm,o,
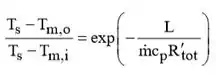
onde é responsável pelas resistências de convecção e de condução da parede do tubo,
E,
Passo 2
Utilizando as correlações e propriedades dos Toolpads da IHT, foram obtidos os seguintes resultados para o efeito do comprimento do tubo L sobre o Tm,o.
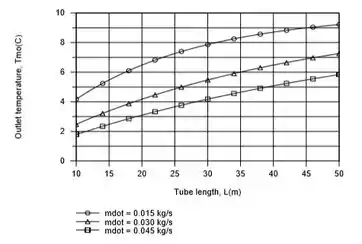
Quanto mais longo o tubo, maior a taxa de extracção de calor do solo, e para m & = 0,030 kg/s, o aumento de temperatura de ΔT = (Tm,o - Tm,i) ≈ 7°C está bem abaixo do valor máximo possível de ΔTmax = 10°C.
Passo 3
(b) O comprimento deve ser de pelo menos 50 m. Se a vazão fosse reduzida em 50% ( m = 0,015 kg/s), o aumento de temperatura correspondente estaria próximo a ΔTmax e L = 50 m estaria próximo do ótimo. No entanto, para a vazão nominal e um aumento de 50% em relação à nominal, o comprimento deve exceder 50 m para recuperar mais calor e fornecer uma temperatura de entrada da bomba de calor que esteja mais próxima do valor máximo possível.
Resposta
Ei, a resposta está no passo a passo :)