Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 39
Ar forçado a e é usado para resfriar elementos eletrônicos em uma placa de circuito. Um desses elementos é um chip, que mede por , localizado a da aresta frontal da placa. Experimentos revelaram que o escoamento sobre a placa é perturbado pelos elementos e que a transferência de calor por convecção é correlacionada por
uma expressão com a forma
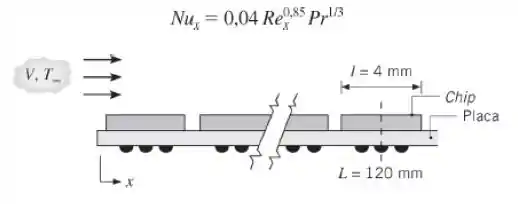
Estime a temperatura superficial do chip se ele estiver dissipando .
Passo 1
Vamos lá! Nosso problema pede a temperatura superficial do chip, mas antes vamos fazer um esboço do nosso problema para facilitar nossa vida.
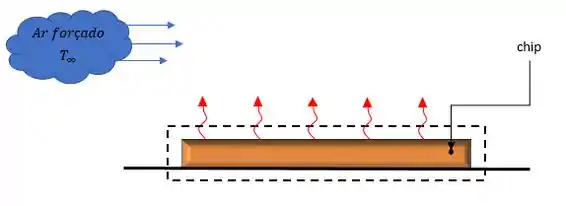
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Vamos lá, vamos usar os dados da tabela , para o ar e assumir que , agora fazendo o balanço de energia temos:
Como estamos no regime permanente e não tem calor entrando por meio de outra superfície.
Seguindo nossa consideração
Usando a lei de convecção de newton temos:
Isolando :
Passo 3
Agora precisamos calcular nosso coeficiente convectivo, vamos considerar que o coeficiente convectivo para toda superfície do chip será uniforme e como estamos avaliando a uma distância , da placa temos:
Assim podemos usar uma relação especial para encontrarmos nosso coeficiente, que fica assim:
Organizando e substituindo pelos dados da tabela e os dados que a questão dá:
Passo 4
Agora vamos só substituir o coeficiente convectivo que encontramos e assim achamos a temperatura:
Sendo temos:
Esse tipo de questão não é muito complicada, só precisamos estar atento as considerações pra facilitar o máximo possível a nossa vida!
Isso é tudo pessoal! \o/
