Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 38
Seja o escoamento paralelo, sobre uma placa plana, de ar a e de óleo de motor a . A velocidade na corrente livre é . A diferença de temperaturas entre a superfície e a corrente livre é a mesma nos dois casos, com .
(a) Determine o local no qual a transição para a turbulência ocorre, , para os dois fluidos.
(b) Para o escoamento laminar sobre uma placa plana, a espessura da camada-limite de velocidade é dada por
Calcule e represente graficamente a espessura da camada-limite de velocidade na faixa , para cada fluido.
(c) Calcule e represente graficamente a espessura da camada-limite térmica para os dois fluidos na mesma faixa de usada na parte (b). Em uma posição na qual os dois fluidos apresentam condições de escoamento laminar, explique qual fluido tem o maior gradiente de velocidade na superfície da placa, . Qual fluido está associado ao maior número de Nusselt local ? Qual fluido está associado ao maior coeficiente de transferência de calor local ?
Passo 1
Vamos lá! Nosso problema nos pede a local onde ocorre a transição de escoamento espessura de camada e propriedades para dois fluídos, óleo e ar, mas antes vamos fazer um esboço do nosso problema para facilitar nossa vida.
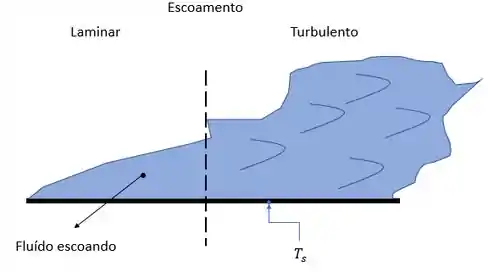
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá, vamos usar os dados da tabela para o ar e os dados da tabela para o óleo de motor, como a transição ocorre em para o número critico de Reynolds , temos:
Para o ar:
Para o óleo de motor:
Passo 3
(b)
Como a espessura da camada-limite de velocidade para o escoamento laminar é dada por:
Usando os dados da tabela para o ar e o óleo temos:
Montando o gráfico para essas duas funções temos:
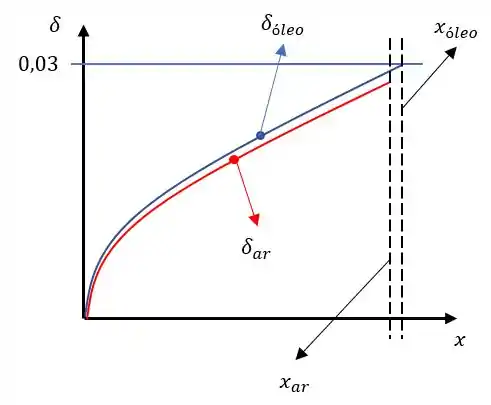
Passo 4
(c)
Como com é dada por:
Usando os dados da tabela para o ar e o óleo temos:
Montando o gráfico para essas duas funções temos:
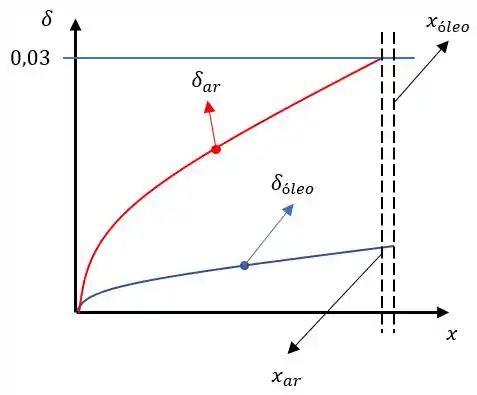
Como representa o espaço em que a temperatura varia da temperatura da placa até a temperatura do entorno do escoamento, o fluído com menor deve ter o maior gradiente de temperatura, imagina nosso como a janela de espaço que a temperatura pode variar, então quanto menor mais a temperatura vai ter que variar pra alcançar a temperatura da outra superfície.
Como ambos os fluídos estão expostos a mesma diferença de temperatura o óleo tem maior gradiente de temperatura, o fluído com maior gradiente de temperatura também terá o maior número de Nusselt, pois:
Assim o óleo terá o maior número de Nusselt.
Por fim como o óleo tem maior coeficiente condutivo e maior número de Nusselt também terá maior coeficiente convectivo tendo em vista que !
Isso é tudo pessoal! \o/
Resposta
(a) .