Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 121

Considere duas placas, A e B, que estão, cada uma, inicialmente isotérmicas e têm espessura L   =   5   m m . As faces das placas são subitamente colocadas em contato em um processo de união. O material A é acrílico, inicialmente a T i , A   =   20 ° C , com ρ A   =   1990   k g / m 3 , c A   =   1470   J / ( k g   ·   K ) e k A   =   0,21   W / ( m   ·   K ) . O material B é aço, inicialmente a T i , B   =   300 ° C , com ρ B   =   7800   k g / m 3 ,   c B   =   500   J / ( k g   ·   K ) e k A   =   45   W / ( m   ·   K ) . As superfícies do acrílico e do aço opostas às da união estão isoladas termicamente. Desprezando a resistência térmica de contato entre as placas, determine quanto tempo levará para a temperatura da superfície do acrílico, oposta à da união, atingir sua temperatura de amolecimento, T a m o l e   =   90 ° C . Represente graficamente a temperatura desta superfície do acrílico, bem como as temperaturas médias dos dois materiais ao longo do intervalo de tempo 0   ≤   t   ≤   300   s . Use 20 pontos nodais igualmente espaçados.

Passo 1

Vamos lá! Nosso problema pede a distribuição de temperatura em forma de gráfico, mas antes vamos fazer um esboço para facilitar nossa vida.

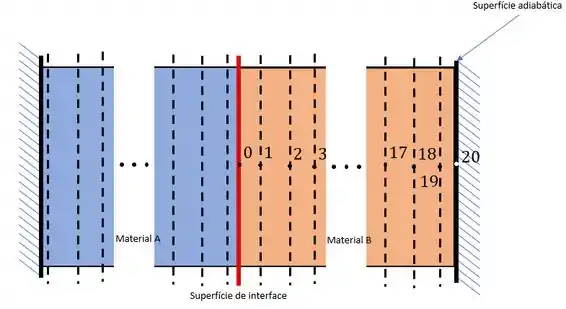
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - C o n d u ç ã o   u n i d i m e n s i o n a l

I I - P r o p r i e d a d e s   c o n s t a n t e s

I I I - R e s i s t e n c i a   d e   i n t e r f a c e   d e s p r e z í v e l

Passo 2

Vamos lá, precisamos fazer a análise para os 20 nós:

Nos nós interiores, m = 2 ,   3 ,   4 ,   … , 17 ,   18 ,   19   19 .

Para o material A

ρ A c A ⋅ Δ y ⋅ T n p + 1 - T n p Δ t = k A T n - 1 p + 1 - T n p + 1 Δ y + k A T n + 1 p + 1 - T n p + 1 Δ y

Para o material B

ρ B c B ⋅ Δ y ⋅ T n p + 1 - T n p Δ t = k B T n - 1 p + 1 - T n p + 1 Δ y + k B T n + 1 p + 1 - T n p + 1 Δ y

No nó central, m = 1 .

ρ A c A ⋅ Δ y 2 ⋅ T 1 p + 1 - T 1 p Δ t = k A T 11 p + 1 - T 1 p + 1 Δ y + k B T 2 p + 1 - T 1 p + 1 Δ y

E nos nós de superfície, m = 10 ,   20 .

Para o material B

ρ A c A ⋅ Δ y 2 ⋅ T 1 0 p + 1 - T 10 p Δ t = k B T 9 p + 1 - T 1 0 p + 1 Δ y

Para o material A

ρ B c B ⋅ Δ y 2 ⋅ T 20 p + 1 - T 20 p Δ t = k A T 19 p + 1 - T 20 p + 1 Δ y

Passo 3

A resistência térmica é dada por:

R t ' ' = Δ y 2 k A + Δ y 2 k B

Podemos notar que a temperatura média pode ser escrita como:

T - = 1 L ∫ 0 L T y d y

Ou pelo método de elementos finitos:

T - A = 1 L A T 11 Δ y 2 + T 12 Δ y + T 1 3 Δ y + T 1 4 Δ y + T 1 5 Δ y + T 1 6 Δ y + T 1 7 Δ y + T 1 8 Δ y + T 1 9 Δ y + T 20 Δ y

e

T - B = 1 L A T 1 Δ y 2 + T 2 Δ y + T 3 Δ y + T 4 Δ y + T 5 Δ y + T 6 Δ y + T 7 Δ y + T 8 Δ y + T 9 Δ y + T 1 0 Δ y

Passo 4

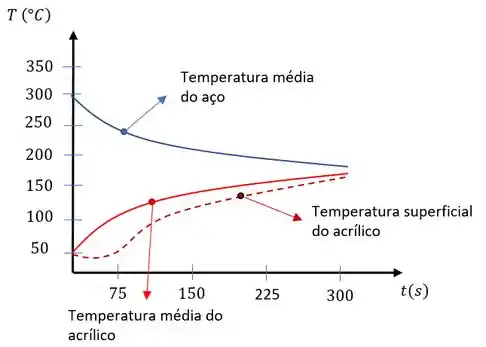
Agora usando qualquer software e inserindo os dados na questão e nossa equação nosso gráfico fica assim:

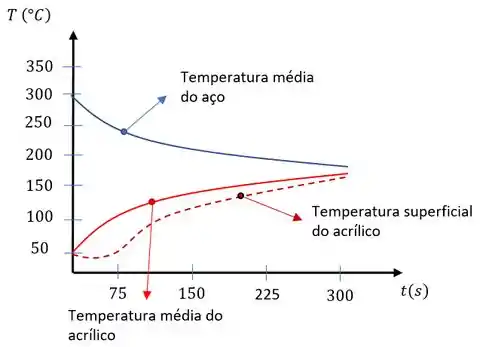
Isso é tudo pessoal! \o/

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As superfícies superior e inferior de uma barra de condução são resfriadas por convecção com ar a T ∞ , com h s ≠ h i . As laterais são resfriadas pela manutenção de contato com sumidouro de calor a T
Seja a malha bidimensional ( ∆ x = ∆ y ) representando condições de regime estacionário, sem geração volumétrica interna de calor, em um sistema com condutividade térmica k . Um dos contornos é mantid
Determine as expressões para q ( m - 1 , n ) → ( m , n ) ,q m + 1 , n → ( m , n ) ,q m ,n + 1 → ( m , n ) e q m ,n - 1 → ( m , n ) , na condução associada a um volume de controle que abrange dois dife
Deduza as equações de diferenças finitas nodais para as seguintes considerações.(a) Nó (m,n) sobre um contorno diagonal sujeito à convecção com um fluido a uma temperatura T ∞ , com um coeficiente de
Seja uma aleta unidimensional, com área de seção transversal uniforme, isolada na sua extremidade, x = L . A temperatura na base da aleta T b e a do fluido vizinho T ∞ , bem como o coeficiente de tran