Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 159

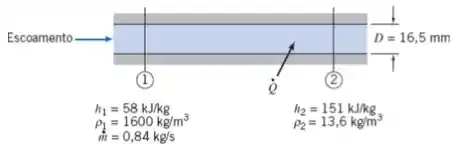
Freon líquido, usado para resfriar componentes elétricos, escoa em regime permanente em um tubo horizontal de diâmetro constante, D = 16,5   m m . Calor é transferido para o escoamento e o líquido ferve, deixando o tubo como vapor. Os efeitos de atrito são desprezíveis comparados com os da adição de calor. As condições do escoamento são mostradas. Determine:

  1. A taxa de transferência de calor;
  2. A diferença de pressão, p 1 - p 2 .

Passo 1

Letra a)

Pela continuidade, temos que:

m ˙ = ρ 1 A V 1

Isolando V 1 :

V 1 = m ˙ ρ 1 A = 4 m ˙ ρ 1 π D 2

Sendo:

D = 16,5   m m = 0,0165 .

ρ 1 = 1600   k g / m 3 ;

m ˙ = 0,84   k g / s .

Temos:

V 1 = 4 ⋅ 0,84 1600 ⋅ π ⋅ 0,0165 2 = 2,46   m / s

Passo 2

Do mesmo modo:

m ˙ = ρ 2 A V 2

Isolando V 2 :

V 2 = m ˙ ρ 2 A = 4 m ˙ ρ 2 π D 2

Sendo:

ρ 2 = 1 3,6   k g / m 3 .

Temos:

V 2 = 4 ⋅ 0,84 13,6 ⋅ π ⋅ 0,0165 2 = 2 88,86   m / s

Passo 3

A Equação de Energia se dá:

Q = m ˙ h 2 + V 2 2 2 - h 1 + V 1 2 2

Sendo:

h 1 = 58   k J / k g ;

h 2 = 151   k J / k g .

Temos:

Q = 0,84 ⋅ 151 + 288,86 2 2 - 58 + 2,46 2 2 = 35   k J / s

Passo 4

Letra b)

Determinando a diferença de pressão, p 1 - p 2 :

p 1 A - p 2 A = m ˙ V 2 - m ˙ V 1

p 1 - p 2 = m ˙ A V 2 - V 1

p 1 - p 2 = 4 m ˙ π D 2 V 2 - V 1

Substituindo os dados:

p 1 - p 2 = 4 ⋅ 0,84 π ⋅ 0,0165 2 288,86 - 2,46 = 1,13   M P a

Resposta

Q = 35   k J / s

p 1 - p 2 = 1,13   M P a

Ver Outros Exercícios desse livro