Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 99

Gás argônio entra em um duto com área de seção transversal constante a M a 1   =   0,2 , P 1 =   320   k P a   e   T 1   =   400   K a uma taxa de 0,8   k g / s . Desprezando as perdas por atrito, determine a mais alta taxa de transferência de calor para o argônio sem reduzir a vazão em massa.

Passo 1

Pra começar com o pé direito, vamos desenhar um esqueminha pra visualizar melhor a questão:

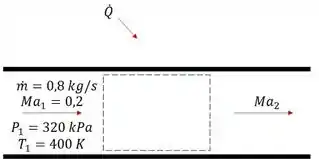
A gente quer achar o valor de Q ˙ mais alto possível sem que a vazão mássica seja reduzida, e como a gente faz isso?!

Primeiro a gente tem que lembrar que quando M a = 1 o fluido esta em estado crítico, e quando aumentamos a velocidade do fluido a vazão diminui, com isso podemos dizer que:

M a 2 = 1

Agora vamos atrás de Q ˙ para M a 2 = 1 !!

Passo 2

Temos que:

Q ˙ = m ˙ c p ( T 02 - T 01 )

c p é tabelado:

c p = 0,5203 k J k g   K

Precisamos achar as temperaturas de estagnação T 01 e T 02 !

Passo 3

Para achar T 01 :

T 01 = T 1 1 + k - 1 2   M a 1     2  

Para o argônio k = 1,667

T 01 = 400 1 + 1,667 - 1 2   0,2 2 = 405,3   K

Passo 4

Para achar T 02 a gente tem que ter uma sacadinha!! M a 2 = 1 , certo?! Então você concorda que T 02 = T 0 * ?!

Então, se a gente achar T 0 * achamos T 02 !!!! Podemos usar a seguinte relação:

T 01 T 0 * = k + 1 M a 1 2 2 + k - 1 M a 1 2 1 + k M a 1 2 2

Substituindo T 0 * por T 02 e isolando:

T 02 = 405,3 × 1 + 1,667 × 0,2 2 2 1,667 + 1 0,2 2 2 + 1,667 - 1 0,2 2

T 02 = 2133   K

Passo 5

Agora podemos achar Q ˙ :

Q ˙ = m ˙ c p ( T 02 - T 01 )

Substituindo:

Q ˙ = 0,8 × 0,5203 2133   - 405,3 = 719,13   k W

Q ˙ = 719   k J

Resposta

Q ˙ = 719   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-19 Uma única onda é iniciada no mar por forte solavanco durante um terremoto. Considerando a profundidade média da água de 2 km e a densidade da água do mar de 1,030 kg/m^3 determine a velocidade d
13-8C Em canais abertos, como é definido o raio hidráulico? Conhecendo o raio hidráulico, como o diâmetro hidráulico do canal pode ser determinado?
13-12C Observa-se que o escoamento em um canal aberto sofreu um salto hidráulico. O escoamento a montante do salto é necessariamente supercrítico? O escoamento a jusante do salto é necessariamente sub
13-18 Água a 10®C escoa em um canal circular com 3 m de diâmetro cheio até a metade a uma velocidade média de 2,5 m/s. Determine o raio hidráulico, o número de Reynolds e o regime de escoamento (lamin
13-16 Água a 15®C escoa de modo uniforme em um canal retangular com 2 m de largura a uma velocidade média de 4 m/s. Se a profundidade da água for 8 cm, determine se o escoamento será subcrítico ou sup