Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 111

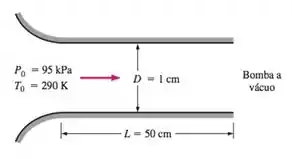
Ar de uma sala a T 0 = 290   K e P 0 = 95   k P a é retirado de forma constante por uma bomba a vácuo através de um tubo adiabático com 1 cm de diâmetro, 50 cm de comprimento e um bocal convergente na entrada. O escoamento na seção do bocal pode ser considerado isentrópico, e o fator de atrito médio do duto pode ser considerado 0,018. Determine a taxa máxima de escoamento de massa do ar que pode ser sugado através desse tubo e o número de Mach na entrada do tubo.

Passo 1

Fala ai! Pra resolver essa questão primeiro temos que assumir algumas coisas já que estamos falando de escoamento de Fanno: estado estacionário, escoamento com atrito constante, gás ideal com propriedades contantes.

Além disso, algumas propriedades do ar a gente vai ter que saber (ou pesquisar hehe):

k = 1,4

c p = 1,005   k J / k g . K

R = 0,287   k J / k g . K

O fator de atrito já foi dado f = 0,0 18 .

Passo 2

Primeiro precisamos saber que a vazão mássica vai ser máxima quando o escoamento for afunilado. Por consequência, o número de Mach na saída vai ser M a 2 = 1. A gente vai poder então igualar a função f L * D h .

f L 1 * D h = f L 1 D h = 0,018   x   0,5 0,01 = 0,9

Lá na tabela A-16 o valor correspondente de Mach pra esse valor é M a 1 = 0,5225 .

Passo 3

Agora a gente precisa saber as condições na entrada, pra poder a vazão máxima na entrada. Como o escoamento é isentrópico, a relação das propriedades termodinâmicas é dada por essas relações:

T 1 = T 01 1 + k - 1 2 M a 1 2 - 1 = 290 1 + 1,4 - 1 2 0,5225 2 - 1 = 275   K

P 1 = P 01 1 + k - 1 2 M a 1 2 - k / ( k - 1 ) = 95 1 + 1,4 - 1 2 0,5225 2 - 1,4 / ( 1,4 - 1 ) = 78,87   k P a

ρ 1 = P 1 R T 1 = 78,87 0,287   x   275 = 0,9993   k g / m ³

Passo 4

Agora que temos os dados da entrada do fluido, podemos calcular a taxa mássica de escoamento.

m ˙ a r = ρ 1 A 1 V 1

V 1 = M a 1 c 1

Onde c 1 = k R T 1

Então bora calcular, sem esquecer de converter as unidades!

c 1 = 1,4   x   0,287   x   275   ( 1000 ) = 332,4   m / s

V 1 = 0,5225   x   332,4 = 173,7   m / s

m ˙ a r = 0,9993   π   0,01 2 4 173,7 = 0,0136   k g / s

Resposta

M a 1 = 0,5225

m ˙ a r = 0 , 0136 k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A baía de Narragansett tem aproximadamente 33,8 km de comprimento e uma profundidade média de 12, 8 m. Cartas de maré para a área indicam um atraso de 30 min entre a maré alta na embocadura (Newport,
A fórmula para a velocidade de propagação de ondas em águas rasas, equação 10.9 ou 10.10, independe das propriedades físicas do líquido, isto é, a massa específica, a viscosidade ou a tensão superfici
Uma onda se propaga com altura de 12 cm em água com uma profundidade de 1,1 m. Calcule (a) a velocidade de propagação e (b) a velocidade induzida δ V .
Água escoa rapidamente em um canal de 25 cm de profundidade. Ao se penetrar a superfície livre com a ponta de um lápis, forma-se uma onda a jusante em formato de cunha com um ângulo total de 38°. Calc
Pedras lançadas sucessivamente no mesmo ponto, dentro do escoamento de água em um canal com 65 cm de profundidade, criam duas ondas circulares, como na figura abaixo. Com base nessa informação, calcul