Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 48

Gás hélio é armazenado a 293 K e 500 kPa em um tanque esférico de 1 cm de espessura e 2 m de diâmetro interno de sílica fundida ( S i O 2 ) . A área onde está localizado o recipiente é bem ventilada. Determine (a) a vazão mássica do hélio por difusão através do tanque e (b) a queda de pressão do tanque em uma semana como resultado da perda de gás hélio.

Passo 1

Animados para mais uma??

Então bora continuar !

Antes de qualquer coisa vamos ver como se calcula a vazão mássica:

m d i f u s ã o ˙ = M M H e × N d i f u s ã o ˙

Já sabemos que:

M M H e = 4,003 k g k m o l

Agora o que nós precisamos achar é a vazão molar do hélio através do recipiente esférico, não é?

Passo 2

Como o recipiente é esférico ele é calculado como:

N d i f u s ã o ˙ = 4 π r 1 r 2 D A B C A ,   1 - C A , 2 r 2 - r 1

Vamos ver o que sabemos?

D A B = 4 , 0 × 10 - 1 4 m 2 s

r 1 = D 1 2 = 2   m 2 = 1   m

r 2 - r 1 = 0,0 1   m → r 2 = 1 m + 0,0 1 m = 1 , 01 m

Como não há hélio do lado externo:

C A , 2 = 0 k m o l m 3

A única coisa que não temos a concentração molar dentro da esfera!

Bora ver como?

C A , 1 = ξ × P H e

Onde ξ é a solubilidade.

Nós sabemos que:

P H e = 5 0 0   k P a × 1 b a r 100   k P a = 5   b a r

E quanto a solubilidade?

Simples !! Vamos olhar a tabela abaixo:

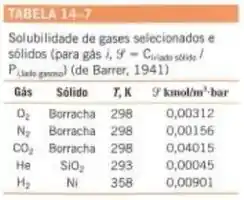
Então:

ξ = 0,00 045 k m o l m ³ . b a r

Agora é só calcular a concentração molar:

C A , 1 = 0,00045 k m o l m 3 . b a r 5   b a r

C A , 1 = 0,00 225 k m o l m ³

Olha que foooda!! Agora só lançar na fórmula da vazão molar:

N d i f u s ã o ˙ = 4 π 1 , 0 m 1,01   m 4,0 × 10 - 14 m 2 s 0,00225 k m o l m ³ - 0 k m o l m 3 0,0 1   m

N d i f u s ã o ˙ = 11,42 × 10 - 1 4 k m o l s

Com a vazão molar agora nós podemos colocar na fórmula do Passo 1 e achar nossa resposta:

m d i f u s ã o ˙ = 4,003 k g k m o l 11,42 × 10 - 14 k m o l s

m d i f u s ã o ˙ = 45,71 × 10 - 1 4 k g s

Então já achamos a resposta para a letra (a)!!

Bora pra (b)?

Passo 3

Na letra (b) nós queremos a queda de pressão do tanque em uma semana como resultado da perda de gás hélio, certo?

A queda de pressão está relacionada ao número de mols, vamos ver ?

P V = n R T

Isolando o número de mols:

n = P V R T

Nós sabemos que:

R = 8,314 k J k m o l . K

T = 293   K

P = 500   k P a

E o volume?

V = 4 3 π r 1 ³

Substituindo:

V = 4 3 π 1   m 3 = 4,189   m ³

Então o volume inicial de mols do hélio era:

n = 500   k P a 4,189   m ³ 8,314 k J k m o l . K 293   K

n = 0,86   k m o l

Então inicialmente tínhamos 0,86 kmol, e quanto nós perdemos ao longo de uma semana?

Sabemos que ele varia a uma vazão molar:

N d i f u s ã o ˙ = 11,42 × 10 - 14 k m o l s

Ao longo de uma semana:

N d i f u s ã o ,   s e m a n a ˙ = 11,42 × 10 - 14 k m o l s × 7   d i a s 1   s e m a n a × 24   h 1   d i a × 3600   s 1   h o r a

N d i f u s ã o ,   s e m a n a ˙ = 6,9 × 10 - 8 k m o l s e m a n a

Sendo assim, o tanque perdeu ao longo de uma semana 6,9 × 10 - 8   k m o l !

Vamos ver quanto sobrou?

n s o b r o u = 0,86   k m o l - 6,9 × 10 - 8   k m o l

n s o b r o u ≅ 0,86   k m o l

Se o número de mols não variou, a pressão também não !!

E a nossa resposta será:

∆ P = 0

O que acharam?

Bem legal, não é?!

Resposta

  1. 45,71 × 10 - 14 k g s ;
  2. ∆ P = 0 .
Ver Outros Exercícios desse livro