Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 119
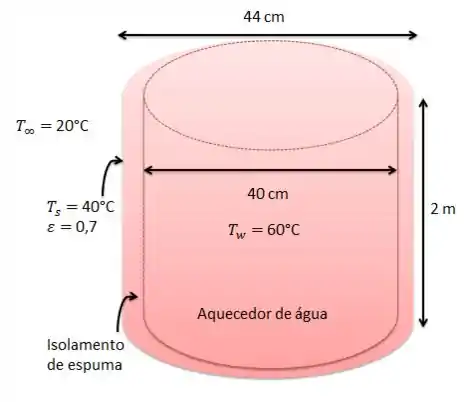
Considere um aquecedor elétrico de água quente que tem 2 m de altura, 40 cm de diâmetro e mantém a água quente a 60°C. O reservatório está situado em uma pequena sala a 20°C cujas paredes e o teto estão mais ou menos na mesma temperatura. O reservatório é colocado em uma casca da placa metálica de espessura desprezível, de 44 cm de diâmetro, e o espaço entre o reservatório e a casca é preenchido com espuma de isolamento. A temperatura média e a emissividade da superfície externa da casca são 40°C e 0,7, respectivamente. O preço da eletricidade é de US$ 0,08/kWh. Um kit de isolamento de reservatórios de água quente, de tamanho suficiente para envolver todo o tanque, está disponível no mercado por cerca de US$ 60,00. Se o tal isolamento for instalado nesse tanque de água pelo proprietário da casa, quanto tempo levará para que o isolamento adicional se pague? Desconsidere qualquer perda de calor a partir das superfícies superior e inferior e considere que o isolamento térmico reduz as perdas em 80%.
Passo 1
Primeiro vamos reunir as informações que temos. Sabemos que o ar ambiente está a uma temperatura 20°C e que a superfície da casca cilíndrica tem temperatura 40°C e emissividade 0,7. O aquecedor perde energia para o ambiente e, sabemos que as perdas com o isolante são 80% menores que as perdas sem o isolante. As dimensões da casca são 44 cm e 2 m. Para instalar a casca cilíndrica o proprietário deve desembolsar US$ 60,00 e, em algum tempo o investimento vai se pagar devido à economia de energia que o isolante proporciona. O exercício nos pede para encontrar qual é esse tempo.
Tudo bem até aqui? Então vamos esquematizar o problema.
Vamos calcular a perda de energia por convecção natural e radiação do sistema com isolante; usar este valor e a informação que o isolamento reduziu a perda em 80% para encontrar a perda de calor sem o isolante; calcular a diferença das perdas; multiplicar a diferença pelo custo da energia; e, por fim, encontrar o número de horas necessárias para que os US$ 60,00 sejam pagos.
Pronto? Vamos lá!!!
Passo 2
Vamos começar pela perda de energia por convecção natural. Para isso, precisamos das propriedades do ar na temperatura de filme. Já vimos que a temperatura média da superfície é 40°C e que a temperatura do ar externo é 20°C. Então, a temperatura de filme fica:
Nesta temperatura as propriedades do ar são:
Queremos determinar a taxa de transferência de calor por convecção natural. Ela pode ser calculada por:
Temos condições de calcular a área superficial do duto e o , mas ainda precisamos do coeficiente convectivo. Uma das maneiras de encontrá-lo é utilizando a correlação de Nusselt para um cilindro vertical:
Precisamos dos adimensionais e . Já temos o número de Prandtl da tabela de propriedades do ar. Vamos para o número de Rayleigh:
Já temos todas as variáveis necessárias para o número de Nusselt. Então vamos calcular :
Agora, vamos calcular a área superficial do cilindro:
Substituindo estes valores na equação da taxa de transferência:
Iremos agora para o cálculo da perda de energia por radiação.
Portanto, a perda de energia com o isolante é:
Sabemos que essa perda corresponde a uma redução de 80% em relação às perdas sem isolamento. Então a perda sem isolamento é:
Passo 3
A diferença entre as perdas de energia sem e com isolamento correspondem à economia de energia. Então:
O custo da energia elétrica é de US$ 0,08/kWh. Então, para encontrar o custo devemos multiplicar este valor por potência (kW) e tempo (h). Queremos encontrar o tempo em que o custo seja de US$ 60,00. Então:
Resposta
Então, o aquecedor se paga em