Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 149

Em gasodutos longos de área constante, como os usados para gás natural, a temperatura é praticamente constante. Considere que o gás deixe uma estação de bombeamento a 350   k P a e 20 º C , com M   =   0,10 . Para a seção ao longo do tubo onde a pressão caiu para 150   k P a , calcule o número de Mach do escoamento. Calor é adicionado ou removido do gás no trecho entre as tomadas de pressão? Justifique a sua resposta: esboce o processo em um diagrama T s . Indique (qualitativamente) T 01 , T 02 e p 02 .

Passo 1

Fala aí, galera. Vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que, por definição:

h 1 + V 1 2 2 + d Q d M = h 2 + V 2 2 2

T 0 T = 1 + k - 1 2 M 2

m ˙ = ρ V A

Os dados de entrada são:

T 1 = 293 K

p 1 = 350 k P a

M 1 = 0,1

p 2 = 150 k P a

Da equação da continuidade:

m ˙ = ρ 1 V 1 A = ρ 2 V 2 A

ρ 1 V 1 = ρ 2 V 2

Também sabemos que:

p = ρ R T

M = V c

Logo, combinando as equações com a da continuidade:

p 1 R T 1 M 1 c 1 = p 2 R T 2 M 2 c 2

Como sabemos que T 1 = T 2   e c 1 = c 2 , temos que:

p 1 M 1 = p 2 M 2

M 2 = p 1 p 2 M 1 = 0,233

Passo 2

Agora, da energia:

d Q d M = h 2 + V 2 2 2 - h 1 + V 1 2 2 = h 02 - h 01 = c p T 02 - T 01

Como temos que:

T 0 T = 1 + k - 1 2 M 2

Manipulando:

T 0 = T 1 + k - 1 2 M 2

Para T   constante e M 2 > M 1 ,   teremos que T 02 > T 01   e d Q d M > 0 .   Logo, a energia é adicionada ao sistema.

Esboçando:

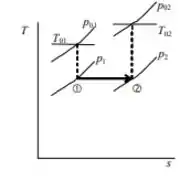
Resposta

M 2 = 0,233

A energia é adicionada ao sistema.

Ver Outros Exercícios desse livro