Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 15.Problemas - Ex. 31
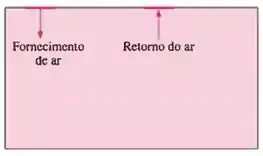
Gere um domínio computacional para estudar a ventilação de uma sala (Figura P15-31). Especificamente, gere uma sala retangular com uma entrada de velocidade no teto para modelar o fornecimento de ar, e uma saída de pressão no teto para modelar o retomo do ar. Você pode fazer uma aproximação bidimensional para simplificar (a sala é infinitamente longa na direção normal à página na Figura P15-31). Use uma malha retangular estruturada. Trace as linhas de corrente e os vetores de velocidade. Discuta.
Passo 1
Fala aí, galerinha. Tudo beleza? Vamos fazer mais uma questão de MecFlu pra tirar aquele na prova. Neste problema devemos executar simulações CFD de fluxo sobre um bloco retangular com vários valores de . Devemos comparar e discutir as linhas de corrente e o coeficiente de arrasto, e devemos comparar nossos resultados de CFD com o valor experimental.
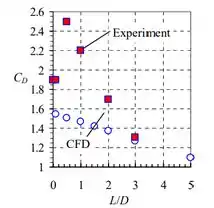
Em primeiro lugar, temos que o escoamento é bidimensional e incompressível, é simétrico em relação ao eixo e é turbulento, mas constante na média. Dado que e , o coeficiente de arrasto é tabulado como uma função de na Tabela 1. Esses dados também são plotados assim:
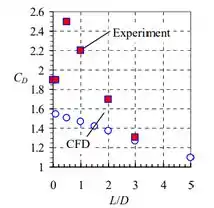
Vemos que os cálculos são consistentemente mais baixos do que os valores experimentais para os comprimentos menores, mas a concordância é muito boa em (tão alto quanto a tabela vai). Enquanto o coeficiente de arrasto obtido experimentalmente atinge o pico em , os cálculos de CFD prevêem que decai continuamente com .
Passo 2
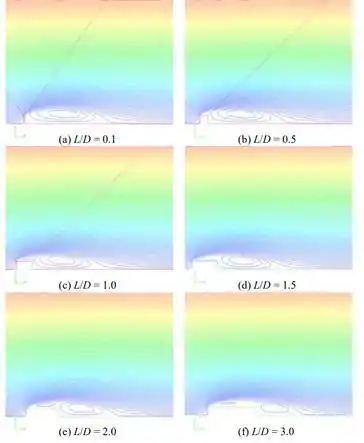
Para vários valores de , plotamos as linhas de corrente perto do bloco:
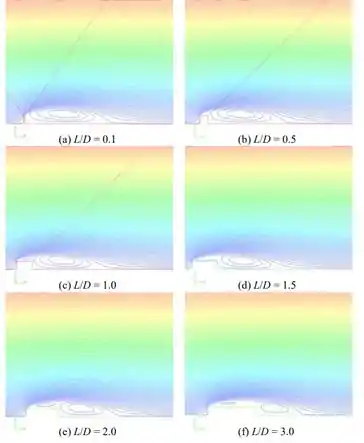
Podemos ver porque o coeficiente de arrasto diminui à medida que aumenta. Nomeadamente, à medida que o comprimento do bloco aumenta, as grandes regiões de fluxo recirculante na esteira (redemoinhos de esteira) diminuem de tamanho (particularmente na direção vertical). Em todos os casos, o fluxo se separa no canto agudo da face embotada, mas conforme aumenta, o fluxo tem mais tempo para achatar ao longo das paredes superior e inferior do bloco, levando a redemoinhos de espessura reduzida.
De fato, por (, o fluxo separado ao longo das paredes superior e inferior parece se reconectar logo a montante da parte de trás do bloco. Os redemoinhos de esteira neste caso são muito mais finos do que aqueles dos blocos mais curtos. Outra forma de expressar isso é dizer que os blocos mais longos são mais “aerodinâmicos” do que os blocos mais curtos e, portanto, têm menos resistência. Experimentos mostram que o arrasto é maior em .
Aparentemente, o processo de liberação de vórtice é forte para este caso, levando a um grande arrasto. Nosso modelo CFD estável e simétrico não é capaz de '' simular os recursos instáveis do fluxo real.
Passo 3
Existem muitas razões possíveis para a discrepância entre os cálculos CFD e a experiência. Estamos modelando o problema como um fluxo constante que é simétrico em relação ao eixo, mas os experimentos revelam que o fluxo sobre corpos escarpados como esses oscilam e desprendem vórtices - o fluxo não é estável nem simétrico. Além disso, estamos usando um modelo de turbulência. Conforme discutido anteriormente, os modelos de turbulência não são universais e podem não ser aplicáveis ao presente problema. Uma simulação de DNS ou LES seria necessária para modelar corretamente os redemoinhos turbulentos instáveis.
É isso, galera. Bora pra praticar mais pra ficar craque.
Resposta
