Um grande tanque de líquido sob pressão é drenado através de um bocal de perfil suave e liso, de área . Considerase que a vazão em massa depende da área do bocal, , da massa específica do líquido, , da diferença de altura entre a superfície do líquido e o bocal, , da pressão manométrica no tanque, e da aceleração da gravidade, . Determine quantos parâmetros independentes podem ser formados para este problema. Determine os parâmetros adimensionais. Enuncie a relação funcional para a vazão em massa em função dos parâmetros adimensionais.
Passo 1
Nessa questão nós temos a relação funcional entre a vazão mássica do líquido de um tanque pressurizado através de um bico com contornos e outros parâmetros físicos.
E com isso queremos encontrar quantos termos independentes que caracterizam esse fenômeno e os termos . Além de informar a relação funcional da vazão mássica em termos dos termos Π. Então vamos lá!
Passo 2
Para resolver essa questão vamos usar o teorema pi de Buckingham. Para o número de parâmetros temos:
![]()
Selecionando as dimensões primárias
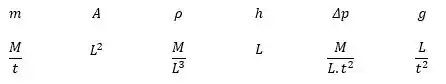
E os parâmetros repetidos:
![]()
Passo 3
Temos grupos sem dimensão. Configurando as seguintes equações dimensionais:
Então,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Verifique usando as dimensões
Passo 4
Para o segundo grupo temos:
Então,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Verifique usando as dimensões
Passo 5
Para o segundo grupo temos:
Então,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Verifique usando as dimensões
A relação funcional é:
Portanto, a taxa de fluxo de massa é: