Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 10.Problemas - Ex. 9
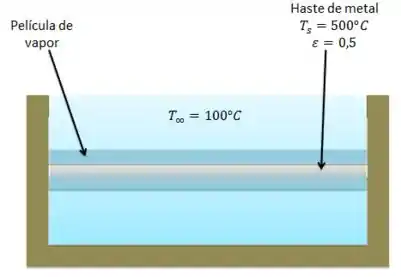
Uma haste cilíndrica de 2 mm de diâmetro com emissividade de 0,5 está submersa na horizontal em água sob pressão atmosférica. Quando a corrente elétrica passa através da haste de metal, a temperatura da superfície atinge 500°C. Determine a dissipação de energia por unidade de comprimento da haste de metal.
Passo 1
Primeiro vamos reunir nossas informações. A haste tem diâmetro 2 mm, temperatura 500°C 773 K e emissividade 0,5. A água está a uma temperatura de 100°C 373 K. Pela imagem vemos também que há uma película de vapor ao redor da superfície, portanto, o regime é de ebulição de película. O exercício pede para determinar a taxa de transferência de calor por comprimento da haste.
Então, o que vamos fazer é: calcular a transferência por radiação; determinar a transferência por convecção em ebulição de película e, no fim, somar as duas taxas e dividir pelo comprimento da haste. Tudo bem? Vamos nessa!!!
Passo 2
Então vamos começar pela taxa de transferência por radiação. Ela é calculada por:
Vamos agora para a transferência de calor por convecção. Mas antes, vamos deixar esquematizadas as propriedades da água líquida a 100°C e do vapor na temperatura de filme.
Para água a 100°C:
Para o vapor, a temperatura de filme é:
Nesta temperatura as propriedades do vapor são:
Com esses dados podemos calcular a taxa de calor pela ebulição em película:
Passo 3
Portanto a taxa de transferência de calor total é:
Como queremos taxa por metro vamos dividir este valor por :
Resposta
A dissipação de energia por comprimento é .