Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 69

Uma instalação de regaseificação de gás natural liquefeito (GNL) utiliza um trocador de calor vertical ou v a p o r i z a d o r , que é constituído por um casco com um feixe tubular de passe único, na conversão do combustível para sua forma vapor para posterior transporte por um gasoduto terrestre. GNL pressurizado é descarregado do navio-tanque e alimentado na base do vaporizador a T f , e n t = – 155 ° C e m ˙ G N L = 150   k g / s , escoando através do casco. O GNL pressurizado tem uma temperatura de vaporização de T v a p = - 75 ° C e calor específico c p ,   l = 4200   J /   ( k g · K ) . O calor específico do gás natural vaporizado é c p , v = 2210   J / ( k g · K ) e o gás tem um calor latente de vaporização de h f g = 575   k J / k g . O GNL é aquecido por água do mar escoando no interior dos tubos, também alimentada pela base do vaporizador e disponível a T q , e n t = 20 ° C , com um calor específico c p , A M = 3985   J / ( k g · K ) . Se o gás deve deixar o vaporizador a T f , s a i = 8 ° C e a água do mar a T q , s a i = 10 ° C , determine a área de transferência de calor requerida para o vaporizador.

Sugestão: Divida o vaporizador em três seções, como mostrado no esquema, com U A = 150   W /   ( m 2 · K ) , U B = 260   W /   ( m 2 · K ) e U C = 40   W /   ( m 2 · K ) .

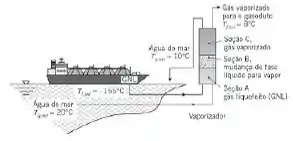
Passo 1

Começamos o problema aplicando um balanço energético para o vaporizador ao todo:

C a l o r   f o r n e c i d o   p e l a   á g u a   d o   m a r = C a l o r   a b s o r v i d o   p e l o   g á s   n a t u r a l

q = q q = q f

m ˙ A M c p , A M T q , e n t - T q , s a i = m ˙ G N L c p , l T v a p - T f , e n t + h f g + c p , v T f , s a i - T v a p  

Calculando a vazão mássica de água do mar:

Dados:

c p , A M = 3985   J / ( k g · K ) ;

T q , e n t = 20 ° C ;

T q , s a i = 10 ° C ;

m ˙ G N L = 150   k g / s ;

T v a p = - 75 ° C ;

T f , e n t = - 155 ° C ;

T f , s a i = 8 ° C ;

c p , l = 4200   J / ( k g · K ) ;

h f g = 575   k J / k g ;

c p , v = 2210   J / ( k g · K ) .

Temos:

m ˙ A M ⋅ 3985 ⋅ 20 - 10 = 150 ⋅ 4200 ⋅ - 75 + 155 + 575 × 10 3 + 2210 ⋅ 8 + 75

m ˙ A M = 4120   k g / s

Calculando a taxa de transferência de calor:

q = m ˙ A M c p , A M T q , e n t - T q , s a i

q = 4120 ⋅ 3985 ⋅ ( 20 - 10 )

q = 164   M W

Passo 2

S e ç ã o   A

Aplicando um balanço de energia para a S e ç ã o   A :

m ˙ A M c p , A M T q , e n t - T q , s a i , 1 = m ˙ G N L c p , l ( T v a p - T f , e n t )  

Substituindo os dados para calcularmos T q ,   s a i ,   1 :

4120 ⋅ 3985 ⋅ 20 - T q , s a i , 1 = 150 ⋅ 4200 ⋅ ( - 75 + 155 )

T q , s a i , 1 = 16,9 ° C

Calculando a taxa de transferência de calor para a S e ç ã o   A :

q A = m ˙ G N L c p , l ( T v a p - T f , e n t )  

q A = 150 ⋅ 4200 ⋅ - 75 + 155

q A = 50,4   M W

A área de transferência de calor necessária da S e ç ã o   A  é calculada com base na diferença de temperatura média logarítmica:

q A = U A A A ∆ T m l

q A = U A A A T q , e n t - T f , e n t - ( T q , s a i , 1 - T v a p ) ln ⁡ T q , e n t - T f , e n t T q , s a i , 1 - T v a p  

Sendo:

U A = 150   W / ( m 2 · K ) .

Temos:

50,4 × 10 6 = 150 ⋅ A A ⋅ 20 + 155 - ( 16,9 + 75 ) ln ⁡ 20 + 155 16,9 + 75  

A A ≅ 2604   m 2

Passo 3

S e ç ã o   C

Aplicando um balanço de energia para a S e ç ã o   C :

m ˙ A M c p , A M T q , e n t , 2 - T q , s a i = m ˙ G N L c p , v ( T f , s a i - T v a p )  

Substituindo os dados para calcularmos T q ,   e n t ,   2 :

4120 ⋅ 3985 ⋅ T q , e n t , 2 - 10 = 150 ⋅ 2210 ⋅ ( 8 + 75 )

T q , e n t , 2 = 11,7 ° C

Calculando a taxa de transferência de calor para a S e ç ã o   C :

q C = m ˙ G N L c p , v ( T f , s a i - T v a p )  

q C = 150 ⋅ 2210 ⋅ 8 + 75

q C = 27,5   M W

A área de transferência de calor necessária da S e ç ã o   C  é calculada com base na diferença de temperatura média logarítmica:

q C = U C A C ∆ T m l

q C = U C A C T q , e n t , 2 - T v a p - ( T q , s a i - T f , s a i ) ln ⁡ T q , e n t , 2 - T v a p T q , s a i - T f , s a i  

Sendo:

U C = 40   W / ( m 2 · K ) .

Temos:

27,5 × 10 6 = 40 ⋅ A C ⋅ 11,7 + 7 5 - ( 10 - 8 ) ln ⁡ 11,7 + 7 5 10 - 8  

A C ≅ 30600   m 2

Passo 4

S e ç ã o   B

Aplicando um balanço de energia para a S e ç ã o   B :

q B = m ˙ G N L h f g  

Calculando a taxa de transferência de calor para a S e ç ã o   B :

q B = 150 ⋅ ( 575 × 10 3 )

q B = 86,25   M W

A área de transferência de calor necessária da S e ç ã o   B  é calculada com base na diferença de temperatura média logarítmica:

q B = U B A B ∆ T m l

q B = U B A B T q , s a i , 1 - T v a p - ( T q , e n t , 2 - T v a p ) ln ⁡ T q , s a i , 1 - T v a p T q , e n t , 2 - T v a p  

Sendo:

U B = 260   W / ( m 2 · K ) .

Temos:

86,25   × 10 6 = 260 ⋅ A B ⋅ 16,9 + 75 - ( 11,7 + 75 ) ln ⁡ 16,9 + 75 11,7 + 75  

A B ≅ 371 6   m 2

Passo 5

A área total de transferência de calor do vaporizador é dada por:

A T o t a l = A A + A B + A C

A T o t a l = 2604 + 3716 + 30600

A T o t a l ≅ 36920   m 2

Resposta

A T o t a l ≅ 36920   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

73 - Considere um trocador de calor no qual ambos os fluidos têm o mesmo calor específico, mas diferentes vazões mássicas. Qual fluido experimentara maior mudança de temperatura: aquele com menor ou m
75 – Em quais condições um trocador de calor de contracorrente pode ter uma efetividade igual a 1?Qual seria sua resposta para um trocador de calor de escoamento paralelo?
81 – Considere um trocador de calor que tem N T U 0,1. Alguém propõe triplicar o tamanho do trocador de calor, e o N T U é triplicado para 0,3, a fim de aumentar a efetividade e, assim, poupar energia
78 - Considere dois trocadores de calor de tubo duplo em contracorrente que são idênticos, exceto que um tem o dobro do comprimento do outro.Qual trocador de calor tem maior probabilidade de ter uma e
79 – Como o N T U de um trocador de calor é definido? O que isso representa? Um trocador de calor com grande N T U (digamos, 10) é necessariamente bom trocador?