Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 133

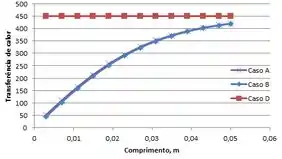
A intensidade na qual a condição na extremidade afeta o desempenho térmico de uma aleta depende da geometria da aleta e de sua condutividade térmica, assim como do coeficiente convectivo. Considere uma aleta retangular de uma liga de alumínio k   =   180 W m K , cuja temperatura na base da aleta é T b = 100 ° C . A aleta está exposta a um fluido com temperatura T ∞ = 25 ° C e um coeficiente convectivo uniforme   h   =   100 W m 2 K pode ser admitido na superfície da aleta.

  1. Para um comprimento da aleta   L   =   10   m m , espessura t   =   1   m m e largura w ≫ t , determine a taxa de transferência de calor na aleta por unidade de largura q ' a , a eficiência η a , a efetividade ε a , a resistência térmica por unidade de largura e a temperatura na extremidade T(L) para os Casos A e B da Tabela 3.4. Compare os seus resultados com aqueles para a aproximação de aleta infinita.
  2. Explore o efeito de variações em L na taxa de transferência de calor para 3 < L < 50   m m . Também considere o efeito de tais variações para uma aleta de aço inoxidável k   =   15 W m .

Passo 1

Bora continuar galeraa !!

Bom, nós queremos achar a a taxa de transferência de calor na aleta por unidade de largura q ' a , ou melhor:

q ' a = q a w

Olhando a Tabela 3.4:

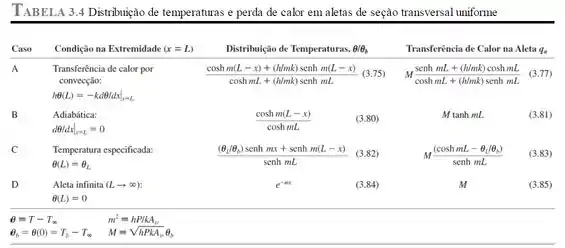
Então nós teremos que analisar três casos, A, B e D:

C a s o   A :         q ' A = M w sinh ⁡ m L + h m k cosh ⁡ m L cosh ⁡ m L + h m k sinh ⁡ m L       e         T x = T ∞ + θ b cosh ⁡ m ( L - x ) + h m k cosh ⁡ m ( L - x ) cosh ⁡ m L + h m k sinh ⁡ m L

C a s o   B :         q ' B = M w tanh ⁡ m L       e         T x = T ∞ + θ b cosh ⁡ m ( L - x ) cosh ⁡ m L

C a s o   D :         q ' D = M w       e         T x = T ∞ + θ b e - m x

Vamos começar calculando nossos parâmetro:

m = h P k A

M = θ b h P k A

Sabendo que:

A = w t

P = 2 w + t

θ b = T b - T ∞

Como w ≫ t :

m = 2 h k t

M = T b - T ∞ 2 w 2 h k t

Vamos ver nossos dados?

k   =   180 W m K

h   =   100 W m 2 K

L   =   10   m m = 0,01   m

t   =   1   m m = 0,001   m

T b = 100 ° C

T ∞ = 25 ° C

Substituindo:

M = 100 ° C - 25 ° C 2 w 2 100 W m 2 K 180 W m K 0,001   m

M = 450 w   W

m = 2 100 W m 2 K 180 W m K 0,001   m = 33,3   m - 1

h m k = 100 W m 2 K 180 W m K 33,3   m - 1 = 0,0167

Agora sim !! Vamos dar início aos trabalhos !!

Passo 2

Vamos começar calculando nossos dados para o Caso A:

q ' A = 450 w w sinh ⁡ ( 33,3   m - 1 × 0,01   m ) + 0,0167 cosh ⁡ ( 33,3   m - 1 × 0,01   m ) cosh ⁡ ( 33,3   m - 1 × 0,01   m ) + 0,0167 sinh ⁡ ( 33,3   m - 1 × 0,01   m )

q ' A = 151 W m

Mas ainda precisamos de alguns dados, certo?

A eficiência pode ser calculada como:

η A = q ' A h ( 2 L + t ) θ b = q ' A h 2 L + t T b - T ∞

A eficácia é dada por:

ε A = q ' A h t θ b = q ' A h t T b - T ∞

E a resistência por unidade de largura:

R ' t ,   A = θ b q ' A = T b - T ∞ q ' A

Substituindo nossos dados:

η A = 151 W m 100 W m 2 K [ 0,02   m + 0,001   m ] 100 ° C - 25 ° C = 0,96

ε A = 151 W m 100 W m 2 K 0,001   m 100 ° C - 25 ° C = 20 , 1  

R ' t ,   A = 100 ° C - 25 ° C 151 W m = 0 , 50 m K W

Mas não era só isso que nós queríamos, certo? Também precisamos da temperatura na extremidade T ( L ) .

Olhando a distribuição da temperatura para o Caso A:

T L = 25 ° C + 100 ° C - 25 ° C cosh ⁡ m ( L - L ) + h m k cosh ⁡ m ( L - L ) cosh ⁡ m L + h m k sinh ⁡ m L

T L = 25 + 75 1 cosh ⁡ ( 33,3   m - 1 × 0,01   m ) + 0,0167 sinh ⁡ ( 33,3   m - 1 × 0,01   m )

T L = 95,6 ° C

Passo 3

Vamos seguir para o Caso B:

q ' B = 450 w w tanh ⁡ ( 33,3   m - 1 × 0,01   m )

q ' B = 450 . tanh ⁡ ( 33,3   m - 1 × 0,01   m )

q ' B = 144 , 0   W m

A eficiência, a eficácia e a resistência por unidade de largura são calculadas do mesmo jeito:

η B = 144 , 0   W m 100 W m 2 K [ 0,02   m + 0,001   m ] 100 ° C - 25 ° C = 0,9 1

ε B = 144 , 0   W m 100 W m 2 K 0,001   m 100 ° C - 25 ° C = 19 , 2  

R ' t ,   B = 100 ° C - 25 ° C 144,0   W m = 0,52 m K W

E agora olhando a distribuição da temperatura para o Caso B:

T L = 25 ° C + 100 ° C - 25 ° C cosh ⁡ m ( L - L ) cosh ⁡ m L

T L = 25 + 75 1 cosh ⁡ ( 33,3   m - 1 × 0,01   m )

T L = 96 ° C

Passo 4

Vamos seguir para o Caso D:

q ' D = 450 w w

q ' D = 450   W m

A eficiência, a eficácia e a resistência por unidade de largura são calculadas do mesmo jeito:

η D = 450   W m 100 W m 2 K [ ∞ + 0,001   m ] 100 ° C - 25 ° C = 0

ε D = 450   W m 100 W m 2 K 0,001   m 100 ° C - 25 ° C = 60  

R ' t ,   D = 100 ° C - 25 ° C 450   W m = 0,167 m K W

E agora olhando a distribuição da temperatura para o Caso B:

T L = 25 ° C + 100 ° C - 25 ° C e - ( 33,3   m - 1 × ∞ )

T L = 25 ° C

Mesmo com a eficiência sendo zero nós podemos comprovar que quando aumentamos o comprimento da aleta nós aumentamos a efetividade da aleta !!

Então finalizamos a letra (a), mas ainda precisamos da (b) !!

Passo 5

Na letra (b) nós queremos explorar o efeito de variações no comprimento na taxa de transferência de calor para 4   <   L   <   50   m m , usando k   =   180 W m K e k   =   15 W m K !!

Então nós faremos tudo que fizemos nos passos anteriores, mas para os diferentes h e usando o valor dado de k, ok?

Quando k   =   180 W m K :

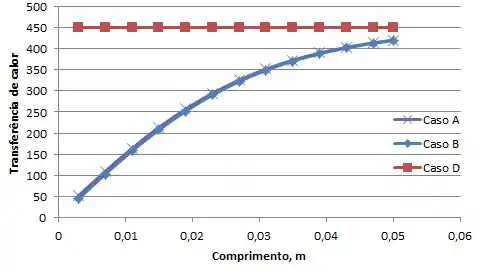
Quando k   =   15 W m K :

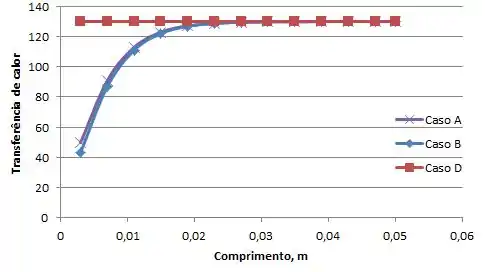
E o que nós concluímos disso?

Para ambos os materiais, existe pouca diferença entre o caso A e B. A grande diferença é observada para o caso D, e quanto menor o k menor a diferença entre os três casos.

Legal, não foi?

Resposta

  1. C a s o   A :   q ' A = 151 , 0 W m         η A = 0,96   ε A = 20,1       R ' t ,   A = 0 , 50 m K W         T L = 95,6 ° C ;

    2. C a s o   B :   q ' B = 144 , 0   W m     η B = 0,9 1   ε B = 19 , 2     R ' t ,   B = 0,52 m K W     T L = 96,0 ° C ;

    C a s o   D :   q ' D = 450,0   W m     η D = 0,0       ε D = 60           R ' t ,   D = 0,167 m K W T L = 25,0 ° C ;

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A intensidade na qual a condição na extremidade afeta o desempenho térmico de uma aleta depende da geometria da aleta e de sua condutividade térmica, assim como do coeficiente convectivo. Considere um
Aletas planas triangulares e parabólicas estão submetidas às mesmas condições térmicas que a aleta plana retangular do Problema 3.134.Determine o comprimento de uma aleta triangular, de largura unitár
Dois longos bastões de cobre, com diâmetro D = 10 mm, serão soldados ponta a ponta com uma solda com ponto de fusão de 650°C. Os bastões encontram-se em um ambiente a 25°C com um coeficiente de transf
Bastões circulares de cobre, com diâmetro D = 1m m e comprimento L = 25m m , são usados para aumentar a transferência de calor em uma superfície mantida a T s , 1 = 100 ° C . Uma extremidade do bastão