Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 137
Bastões circulares de cobre, com diâmetro e comprimento , são usados para aumentar a transferência de calor em uma superfície mantida a . Uma extremidade do bastão é presa a essa superfície (em x = 0), enquanto a outra extremidade (x = 25 mm) é conectada a uma segunda superfície, mantida a . Ar, escoando entre as superfícies (e sobre os bastões), também se encontra a uma temperatura , mantendo um coeficiente convectivo .
- Qual é a taxa de transferência de calor por convecção entre um único bastão de cobre e o ar?
- Qual é a taxa total de transferência de calor dissipada em uma seção da superfície a 100°C, com dimensões de 1 m × 1 m, se for instalado um feixe de bastões com distância entre os centros de 4 mm?
Passo 1
Vamos que vamos galerinhaa??
Olhem de perto o que está acontecendo aqui:
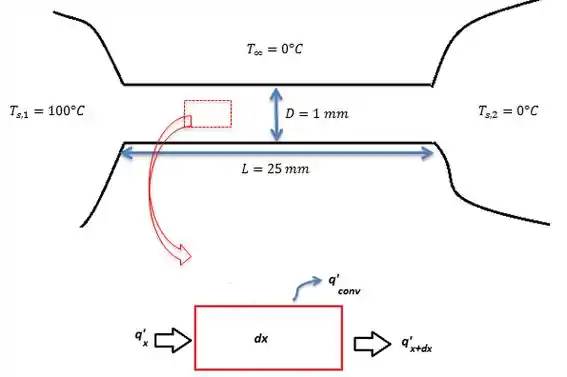
Quando nós fazemos o balanço de energia teremos que o calor sendo adicionado ao volume, , e saindo do volume de controle, e Então:
Agora nós precisamos achar cada um dos termos, ok?
A primeira coisa que devemos fazer aqui é escrever a equação de Fourier para a condução que ocorre a uma distância x:
E para uma distância
A transferência de calor por convecção pode ser dada como:
Agora nós podemos substituir tudo que temos:
Como o dx está presente em todos os termos:
E substituindo
Se nós assumirmos que:
Então:
Na fórmula da letra (a):
Se:
Então:
Quando nós temos uma equação diferencial de segunda ordem com coeficientes constantes a solução é dada pela forma:
Onde:
Aplicando a primeira condição de contorno, quando e , então:
Se nós aplicarmos a segunda condição de contorno, quando e
Isolando
Substituindo na primeira condição de contorno:
Colocando nossas constantes na solução:
Vamos guardar esta informação, ok?
Passo 2
Mas não achamos o que queríamos, certo?
Queremos a troca de calor por convecção, como vimos no Passo 1:
Adaptando o que vimos antes:
Derivando
Substituindo a derivada e a área:
Agora nós vamos calcular o único dado que não temos, m.
Se ele é dado por:
E sabendo que:
Para achar o k nós precisamos da temperatura média:
Olhando na Tabela A.1 nós teremos que:
Substituindo em m:
Na condução:
Quando
Quando
Agora é só achar o calor convectivo:
A letra (a) tá feita galerinha !!
Passo 3
Boom, na letra (b) as aletas são separadas por 4 mm ao longo de uma área de
Para achar o número de aletas devemos dividir o lado pelo espaçamento:
Se um lado nós temos 250 aletas, em uma seção de
A área que não está ocupada pelas aletas é dada por:
Então, a transferência de calor total será a transferência de calor por condução realizada pelas aletas somado à transferência de calor por convecção do espaço livre delas:
Substituindo:
E nós finalizamos mais uma bem puxada, não foi !!