Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 135
Aletas planas triangulares e parabólicas estão submetidas às mesmas condições térmicas que a aleta plana retangular do Problema 3.134.
- Determine o comprimento de uma aleta triangular, de largura unitária, e espessura da base t = 3 mm, que fornecerá a mesma taxa de transferência de calor que a aleta plana retangular. Determine a razão entre as massas da aleta triangular e da aleta retangular.
- Repita a parte (a) para a aleta parabólica.
Passo 1
Vamos seguir galerinhaaa !!
Preparados ??
Vamos dar uma olhada mais de perto nas expressões para cada uma delas:
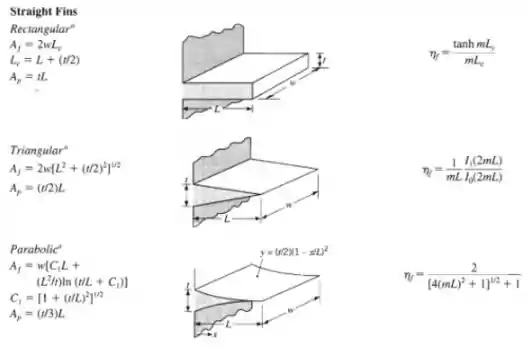
Nós precisamos achar o comprimento de uma aleta triangular que fornecerá a mesma taxa de transferência de calor que a aleta plana retangular e determina a razão entre as massas da aleta triangular e da aleta retangular.
Vamos começar pela aleta retangular, ok? A eficiência pode ser calculada como:
Se:
Como
Sabendo do problema anterior que:
Então:
Na fórmula:
O calor pode ser calculado em função da eficiência:
Como:
Considerando a largura unitária:
Substituindo:
Achamos a transferência de calor da aleta retangular, ok?
Então:
Passo 2
Para a aleta triangular, a eficiência pode ser calculada usando a fórmula dada:
Na fórmula do Passo 1:
Enquanto:
Igualando as duas e substituindo:
Quando nós olhamos as funções de Bessel na Tabela B.5 no Apêndice B nós podemos achar o comprimento desta aleta:
Mas não acabamos né?
Queremos a razão entre as massas:
Substituindo:
Passo 3
E o último perfil é a aleta parabólica, pedida na letra (b)!
Sabendo que:
Para este perfil de aleta nós temos que:
Na fórmula do Passo 1:
Igualando as duas:
Substituindo o que já temos:
Enquanto:
Onde:
Então:
Igualando na equação anterior:
Resolvendo a equação:
Mas não acabamos né?
Queremos a razão entre as massas:
Substituindo:
E finalizamos mais umaa !!