Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 42

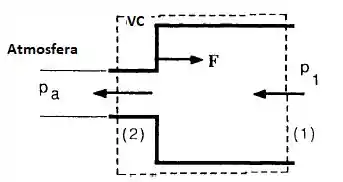
Um líquido de massa específica ρ escoa através da contração brusca da figura abaixo e sai para a atmosfera. Considere condições uniformes ( ρ 1 , V 1 , D 1 ) na seção 1 e ( ρ 2 ,   V 2 ,   D 2 ) na seção 2. Encontre uma expressão para a força exercida pelo fluido sobre a contração.

Passo 1

Vamos juntos encarar mais um capítulo da série “mecflu e seus desafios?” Vem comigo!!

Primeiro, vamos entender o problema. Como estamos saindo para um local com pressão atmosférica, temos que a pressão no ponto 2 é igual a atmosférica. Se subtrairmos a pressão atmosférica em todos os lados do nosso VC, vamos observar que as pressões atmosféricas se cancelam no eixo y e que a única pressão não nula será na seção 1, p = p 1 - p a t m .

Ou seja, ao analisarmos vemos que temos uma força F contrapondo uma força de pressão Fp=pA. Além disso essa diferença de forças deve ser igual a diferença de força exercida pelo escoamento nas duas regiões.

∑ F x = F - p 1 - p a A 1 = m ˙ 2 u 2 - m ˙ 1 u 1

Sabemos que independente da mudança de área transversal, a vazão mássica se mantém!

m ˙ 2 = m ˙ 1 = ρ 1 A 1 V 1

Porém o diferencial é que u 2 = - V 2 e u 1 = - V 1 uma vez que temos seções transversais de escoamento diferentes, suas velocidades de escoamento também serão diferentes.

F = p 1 - p a A 1 + ρ 1 A 1 V 1 V 1 - V 2

Passo 2

Agora que temos V 1 e V 2 precisamos identificar qual é a relação entre essas duas velocidades a partir do balanço de massa!!

Q 1 = Q 2

π 4 D 1 2 V 1 2 = π 4 D 2 2 V 2 → V 2 = V 1 D 1 2 D 2 2

Passo 3

Substituindo dentro do nosso balanço de forças:

F = p 1 - p a A 1 - ρ 1 A 1 V 1 2 D 1 D 2 2 - 1

Lembrando que A 1 = π 4 D 1 2

Resposta

F = p 1 - p a A 1 - ρ 1 A 1 V 1 2 D 1 D 2 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para flutuar no alto de uma montanha, um helicóptero precisa de mais, menos ou da mesma potência que precisaria para flutuar no nível do mar? Explique.
Um jato d’água horizontal de um bocal com seção transversal de saída constante atinge normalmente uma placa plana vertical e fixa. Determinada força F é necessária para manter a placa contra a corrent
Descreva por que um helicóptero flutua no ar em termos do momento e do escoamento de ar.
Um jato d’água horizontal com 5c m de diâmetro e velocidade de 30m / s atinge uma placa plana fixa vertical. A água se espalha em todas as direções no plano da placa. Qual a força necessária para mant
A água entra em uma bomba de escoamento mista axialmente a uma taxa de 0,2m 3 / s e a uma velocidade de 5 m s , e é descarregada para a atmosfera a um ângulo de 60 ° da horizontal, como mostra a figur