Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 28

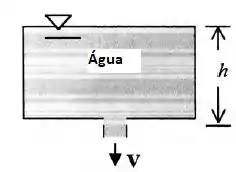
De acordo com o teorema de Torricelli, a velocidade de um fluido escoando por um orifício em um tanque é V ≈ 2 g h 1 2 , em que h é a altura da água acima do orifício. Considere que o orifício tenha uma área A 0 e o tanque cilíndrico tenha uma seção transversal com área A b ≫ A 0 . Deduza uma fórmula para o tempo necessário para esvaziar o tanque completamente a partir de uma altura inicial h o .

Passo 1

Vamos entrar em mais uma guerra com a mecflu? Claro, a gente vai ganhar! Hehe

Bem, vamos partir pro nosso balanço de massa!!!

m ˙ e - m ˙ s = m ˙ a c u m u l a d o = d ρ v ∂ t

Como não temos vazão de entrada, o nosso sistema fica:

m ˙ s + ∂ ρ v ∂ t = 0

A gente agora precisa lembrar que o volume de um tanque será dado pela área da base Ab pela sua altura h, e considerando densidade constante! Além disso, precisamos lembrar que, como dito no enunciado, a velocidade no orifício é dada por 2 g h 1 2 e que ele terá área transversal A0

m ˙ s + ρ A b ∂ h ∂ t = 0 → ρ A b ∂ h ∂ t = - m ˙ s = - ρ A 0 2 g h

Passo 2

Agora vamos resolver nossos paranuês integrando a igualdade, beleza?

∫ h 0 0 d h h = ∫ 0 t A 0 2 g A b d t → t = A b A 0 h o 2 g

Resposta

t = A b A 0 h 0 2 g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bomba de jato abaixo, injeta água a U 1 = 40m / s através e um tubo de 75 mm e promove um escoamento secundário de água, U 2 = 3m / s , na região anular em torno do tubo pequeno. Os dois escoamentos
Um fole pode ser modelado como um volume deformável em forma de cunha, como mostra a figura. A válvula de retenção do lado esquerdo (pregueado) fica fechada durante o sopro. Se b é a largura do fole,
Da teoria elementar do escoamento compressível (Capítulo 9), ar comprimido irá descarregar de um tanque por um orifício, com a vazão em massa ≈ C ρ , em que ρ é a massa específica do ar no tanque e C
Em alguns tuneis de vento, a seção de teste é perfurada para fazer a sucção de ar e manter uma camada-limite viscosa delgada. A parede de seção de teste na figura abaixo contém 1200 orifícios de 5 mm
Um fluido incompressível está sendo espremido entre dois grandes discos circulares, pelo movimento de descida uniforme V 0 do disco superior. Considere escoamento radial, unidimensional, para fora, us