Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 33

O manômetro de tubo inclinado mostrado tem D = 76 mm e d = 8 mm, e está cheio com óleo Meriam vermelho. Calcule o ângulo, θ, que dará uma deflexão de 15 cm ao longo do tubo inclinado para uma pressão aplicada de 25 mm H2O (manométrica). Determine a sensibilidade desse manômetro.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos.

Da equação de fluidos incompressíveis, para a Equação monomérica

∆ P = ρ m e r × g × ∆ h

∆ P = S G m e r × ρ × g × ∆ H                   ( 1 )

Onde

∆ P está a diferença de pressão,

g é a aceleração devido à gravidade,

ρ m e r é a densidade do óleo vermelho Meriam,

ρ é a densidade da água,

∆ h é a diferença de altura.

Da tabela de gravidade específica.

Gravidade específica do óleo vermelho Meriam, S G m e r = 0.827

Passo 2

Agora vamos desenhar o manômetro inclinado

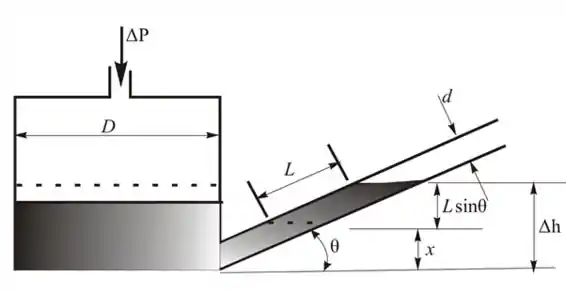
Passo 3

Partindo da figura do passo anterior

∆ h = x + L   s e n   θ

Substiutindo na expressão (1)

∆ h por x + L   s e n   θ

0.827 por S G m e r

1000   k g / m 3 por ρ

∆ P = S G m e r × ρ × g × ∆ H    

∆ P = 0.827 × 1000 × 9.81 × ( L   s e n   θ + x )

∆ P = 8112.87   L   s e n   θ + x             ( 2 )

Para a água

∆ P = ρ g h

∆ P = 1000 × 9.81 × 0.025

∆ P = 245.25   P a

Passo 4

O volume do líquido é constante

V r e s = V t u b

x A r e s = L A t u b

x × π 4 D 2 = L × π 4 d 2

x = L d D 2

Onde D e d , são os diâmetros

Substituindo na expressão (2)

245.25   P a por ∆ P

L d D 2 por x

∆ P = 8112.87   L   s e n   θ + x             ( 2 )

245.25 = 8112.87 L   s e n   θ + L d D 2               ( 3 )

Passo 5

Substituindo na expressão (3)

0.15   m para L ,

0.008   para d

0.076 para D

245.25 = 8112.87 L   s e n   θ + L d D 2

245.25 = 8112.87 0.15   s e n   θ + 0.15 0.008 0.076 2

0.03023 = 0.15   s e n   θ + 0.001662

0.15   s e n   θ = 0.02856

s e n   θ = 0.19045

θ = 10.98 °

O ânguloinclinado de θ   é ≈ 11 ° .

Passo 6

A sensibilidade do manômetro é

s = L h

Substituindo

0.15   m por L ,

0.025 por h .

s = 0.15 0.025

s = 6

Portanto, a sensibilidade do manômetro é de s = 6

Resposta

θ = 11 º

s = 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura P2.11, o medidor de pressão manométrica A indica 1,5 kPa (manométrica). Os fluidos estão a 20°C. Determine as elevações z , em metros, dos níveis dos líquidos nos tubos piezométricos abertos
O tubo em V simétrico na Figura P2.14 contém água estática e ar a 20 °C. Qual é a pressão do ar na parte fechada no ponto B?
Considere que um barômetro, usando tetracloreto de carbono como fluido de trabalho (não recomendado), seja instalado em um dia normal em Denver, Colorado. (a) Até que altura vai subir o fluido no tubo
O sistema na Figura P2.17 está a 20°C. Se a pressão no ponto A é de 90973 Pa, determine as pressões nos pontos B, C e D em Pa.
O sistema ar-óleo-água na Figura P2.15 está a 20°C. Sabendo que o manômetro A registra a pressão absoluta de 103,42 kPa e o manômetro B registra 8618 Pa menos do que o manômetro C, calcule (a) o peso