Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 165

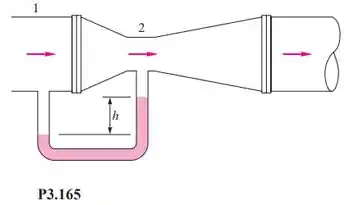
Um medidor Venturi, mostrado na Figura P3.165, tem uma redução de seção cuidadosamente projetada cuja diferença de pressão é uma medida da vazão no tubo. Aplicando a equação de Bernoulli para escoamento permanente, incompressível e sem perdas, mostre que a vazão volumétrica Q relaciona-se à leitura h do manômetro por:

Q = A 2 1 - ( D 2 / D 1 )   4   2 g h ρ M - ρ ρ

em que ρ M é a massa específica do fluido manométrico.

Passo 1

Para resolver esta questão vamos começar calculando a pressão hidrostática no manômetro da imagem, é bem simples:

p 1 - p 2 = ρ M - ρ g h

Pronto, agora vamos aplicar Bernoulli entre 1 e 2, lembrando que os pontos estão na mesma altura, ou seja, ∆ z = 0 :

p 1 + ρ 2 V 1 2 + ρ g z 1 = p 2 + ρ 2 V 2 2 + ρ g z 2

p 1 + ρ 2 V 1 2 = p 2 + ρ 2 V 2 2

p 1 - p 2 = ρ 2 ( V 2 2 - V 1 2 )

ρ M - ρ g h = ρ 2 ( V 2 2 - V 1 2 )

Passo 2

Vamos encontrar uma relação entre V 1 e V 2 para simplificarmos mais nossa expressão. Para isso é só utilizar a equação da continuidade:

Q 1 = Q 2

V 1 * A 1 = V 2 * A 2

V 1 π 4 D 1 2 = V 2 π 4 D 2 2

V 1 = V 2 D 2 D 1 2

Substituindo na nossa expressão:

ρ M - ρ g h = ρ 2 ( V 2 2 - V 1 2 )

ρ M - ρ g h = ρ 2 V 2 2 - V 2 2 D 2 D 1 4

ρ M - ρ g h = ρ V 2 2 2 1 - D 2 D 1 4

Como o exercício pede a vazão vamos precisar isolar a velocidade na nossa expressão:

ρ M - ρ g h = ρ V 2 2 2 1 - D 2 D 1 4

V 2 = 2 ρ M - ρ g h ρ 1 - D 2 D 1 4

Passo 3

Agora é só utilizar a equação da vazão volumétrica. Pela a continuidade, a vazão volumétrica é igual eu todo o escoamento, com isso, vamos calcular a vazão em 2 já que temos V 2 , logo:

Q = A 2 * V 2 = A 2 * 2 ρ M - ρ g h ρ 1 - D 2 D 1 4

Podemos rearranjar parar deixar igual a expressão do enunciado:

Q = A 2 1 - ( D 2 / D 1 )   4   2 g h ρ M - ρ ρ

Resposta

Q = A 2 * 2 ρ M - ρ g h ρ 1 - D 2 D 1 4 = A 2 1 - ( D 2 / D 1 )   4   2 g h ρ M - ρ ρ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Explique como e por que um sifão funciona. Alguém propõe passar com sifão água fria sobre uma parede com 7m de altura. Isso é possível? Explique.
Em determinada aplicação, um sifão deve passar sobre uma parede alta. A água ou o óleo com gravidade específica de 0,8 pode passar sobre uma parede mais alta? Por quê?
O nível de água de um tanque no telhado de um prédio está 20m acima do solo. Uma mangueira vai da parte inferior do tanque até o solo. O final da mangueira tem um bocal, que aponta diretamente para ci
O que é linha piezométrica? Em que ela difere da linha de energia? Sob quais condições ambas as linhas coincidem com a superfície livre de um líquido?
Defina pressão estática, dinâmica e hidrostática. Sob quais condições a soma é constante para uma corrente de escoamento?