Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas para exames de fundamentos de engenharia - Ex. 1
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se a vazão volumétrica é de 606 L/min, qual é a velocidade média na seção 1?
(a) 2,6 m/s, (b) 0,81 m/s, (c) 93 m/s, (d) 23 m/s, (e) 1,62 m/s.
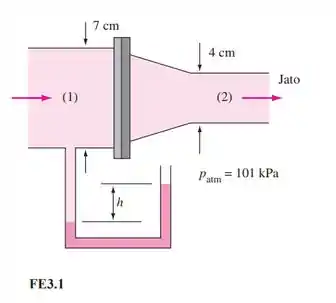
Passo 1
Como a gente pode ver, essa é uma questão bem simples de aplicação da equação da continuidade, certo galera?
Pela equação da continuidade, a vazão em um ponto de um duto é a mesma em qualquer outro ponto dentro deste mesmo tubo. Bora equacionar isso:
O problema nos pediu para achar qual a velocidade em 1, logo, podemos escrever a equação da continuidade da seguinte maneira:
A vazão no ponto dois já foi dada:
Convertendo para m3/s:
A área da seção transversal em 1 pode ser escrita como (lembrando que o diâmetro da seção transversal em 1 é :
Agora é só substituir e achar :
Resposta
Letra A: (a) 2,6 m/s