Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 38

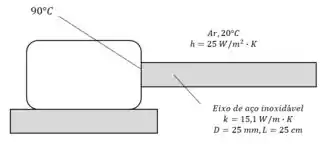
Um motor CD fornece energia mecânica para um eixo de aço inoxidável em rotação k = 15,1 W m ∙ K com comprimento de 25   c m e diâmetro de 25   m m . A temperatura do ar ambiente está em torno de 20   ° C , o coeficiente de transferência de calor por convecção é de 25 W m 2 ∙ K , e a temperatura base do eixo do motor é 90 ° C . Usando um espaçamento nodal uniforme de 5   c m ao longo do eixo do motor, determine as equações de diferenças finitas e as temperaturas nodais, resolvendo as equações.

Passo 1

Anotando os dados do enunciado:

∆ x = 5   c m ; k = 15,1 W m ∙ K ; T ∞ = 20 ° C ,   T 0 = 90 ° C ,   h = 25 W m 2 ∙ K ; D = 25   m m ; L = 25   c m  

Agora podemos calcular o número de nós para o nosso problema.

M = L ∆ x + 1 = 25   c m 5   c m + 1 = 6

Muito bem!! Note que nosso nó 0 é referente a T 0 = 90 ° C , logo...

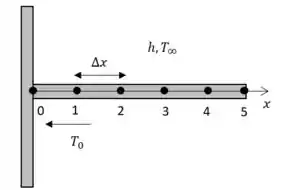
Bom, a partir da representação podemos usar nossa equação geral de diferenças finitas para se obter uma expressão para os nós interiores 1, 2, 3 e 4.

k A T m - 1 - T m ∆ x + k A T m + 1 - T m ∆ x + h p ∆ x T ∞ - T m = 0

T m - 1 - 2 + h p ∆ x 2 k A T m + T m + 1 + h p ∆ x 2 k A T ∞ = 0

Onde,

h p ∆ x 2 k A = 4 h ∆ x 2 k D = 4 25 W m 2 ∙ K 0,05 2 15,5 W m ∙ K 0,025   m   = 0,6452

Passo 2

Para o nosso nó 5, note que se refere a ponta da aleta e aplicando o balanço de energia podemos chegar na seguinte equação:

k A T 4 - T 5 ∆ x + h p ∆ x 2 + A T ∞ - T 5 = 0

T 4 - 1 + h ∆ x k A p ∆ x 2 + A T 5 + h ∆ x k A p ∆ x 2 + A T ∞ = 0

Onde,

h ∆ x k A p ∆ x 2 + A = h ∆ x k 2 ∆ x D + 1 = 0,4032

Passo 3

Obtido as equações, podemos encontrar a equação apara cada nó.

Para o n ó   1 :

T 0 - 2,6452 T 1 + T 2 + 0,6452 T ∞ = 0

Para o n ó   2 :

T 1 - 2,6452 T 2 + T 3 + 0,6452 T ∞ = 0

Para o n ó   3 :

T 2 - 2,6452 T 3 + T 4 + 0,6452 T ∞ = 0

Para o n ó   4 :

T 3 - 2,6452 T 4 + T 5 + 0,6452 T ∞ = 0

Para o n ó   5 :

T 4 - 1,4032 T 5 + 0,4032 T ∞ = 0

Resposta

Resolvendo as equações simultaneamente, nos encontramos as seguintes temperaturas:

T 1 = 52,03 ° C

T 2 = 34,72 ° C

T 3 = 26,92 ° C

T 4 = 23,58 ° C

T 5 = 22,55 ° C

Ver Outros Exercícios desse livro