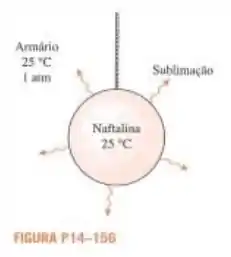
A naftalina é comumente usada como repelente contra traças para proteger o vestuário durante o armazenamento. Considere uma bola de naftalina esférica de 1,5 cm de diâmetro pendurada em um armário a a . Considere a variação do diâmetro com o tempo, determine quanto tempo levará para a naftalina sublimar completamente. A densidade e a pressão do vapor da naftalina a são e , respectivamente, e a difusividade da massa da naftalina no ar a é .
Passo 1
Dados fornecidos:
Temperatura ambiente:
Pressão ambiente:
Diâmetro da esfera de naftalina:
Densidade da naftalina:
Pressão de vapor da naftalina:
Difusividade da massa da naftalina no ar a :
Premissas:
1) A concentração de naftaleno no ar é muito pequena e as condições de baixo fluxo de massa existem para que a analogia de Chilton-Colburn entre transferência de calor e massa seja aplicável (será verificada).
2) O ar e o vapor de naftaleno são gases ideais.
3) O naftaleno e o ar circundante estão na mesma temperatura.
4) Os efeitos da radiação são insignificantes.
Propriedades:
Massa molar do naftaleno:
Massa molar do ar:
Propriedades de ar seco para a mistura a a pela Tabela A-15.
Densidade do ar:
Passo 2
Fala galera!!!
Para resolver essa questão, é importante perceber que o ar que entra é livre de naftalina e, portanto, a fração de massa do naftaleno em condições de corrente livre é zero . Então, como a pressão de vapor da naftalina na superfície é , Podemos calcular a fração de massa de naftalina na lado do ar da superfície. Assim temos:
Aqui, é a pressão de vapor da naftalina na superfície, é a pressão atmosférica, é a massa molar da naftalina e é a massa molar do ar. Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 3
Normalmente, esperamos que as correntes de convecção naturais se desenvolvam ao redor da bola de naftalina, porque a quantidade de naftalina próxima à superfície é muito maior. Então, podemos determinar o número de Nusselt (e sua contrapartida na transferência de massa, o número de Sherwood) pela Eq. 14-16. Assim temos:
Aqui, é o número de Raleigh e é o número de Prandtl.
Temos que o valor da fração de massa determinado acima indica que a quantidade de naftaleno no ar é tão baixa que não causa nenhuma diferença significativa na densidade do ar. Sem gradiente de densidade, não haverá convecção natural e, portanto, o número de Rayleigh pode ser considerado zero. Então a relação do número de Nusselt acima será reduzida para:
Temos então que ou seu equivalente . Então, usando a definição do número de Sherwood, o coeficiente de transferência de massa pode ser expresso da seguinte maneira:
Passo 4
Podemos expressar a massa da bola de naftalina da seguinte maneira:
Aqui, é a densidade da naftalina e é o volume da bola de naftalina . Assim temos:
Passo 5
Temos que a taxa de variação da massa de naftaleno é igual à taxa de transferência de massa do naftaleno para o ar. Assim, podemos expressar essa igualdade da seguinte forma:
Aqui, é a área da superfície da bola . Substituindo os termos da equação acima pelos dados obtidos, temos:
Passo 6
Agora, vamos integrar a relação encontrada no passo anterior para obter uma relação de tempo necessário para a sublimação da naftalina.
Integrando a equação com limites de diâmetro variando de até e limites de tempo variando de até . Assim temos:
Passo 7
Agora, vamos usar a relação acima para determinar o tempo que leva para a naftalina sublimar completamente. Assim temos;
Portanto, o tempo necessário para a sublimação completa da naftalina é .