Um navio deve ser movido por um cilindro circular rotativo. Testes de modelo são planejados para estimar a potência requerida para girar o cilindro protótipo. Uma análise dimensional é necessária para transportar por escala os resultados dos testes do modelo para o protótipo. Liste os parâmetros que deveriam ser incluídos na análise dimensional. Faça uma análise dimensional para identificar os grupos adimensionais importantes.
Passo 1
Nessa questão nós temos uma embarcação a ser alimentada por um cilindro circular rotativo. Os testes do modelo são planejados para determinar a potência necessária para o protótipo.
A partir disso queremos encontrar a lista de parâmetros que devem ser incluídos na análise e realizar análise dimensional para identificar os importantes grupos adimensionais
Passo 2
De uma inspeção do problema físico:
Agora usaremos o teorema pi de Buckingham para encontrar os grupos sem dimensão. Começando pelos parâmetros:
![]()
Selecionando as dimensões primárias :
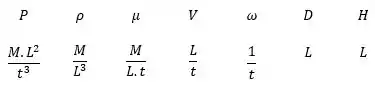
E os parâmetros repetidos:
![]()
Passo 3
Então nós temos grupos sem dimensão. Configurando as equações dimensionais:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 4
Para o segundo grupo temos:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 5
Para o terceiro grupo temos:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 6
Para o quarto grupo temos:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 7
Verificando usando as dimensões :
A relação funcional é:
Então,