Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 11

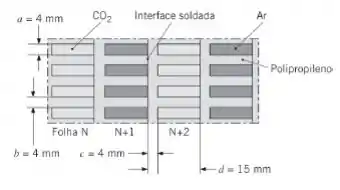
Um novo conceito de trocador de calor consiste em um grande número de folhas de polipropileno extrudado (k = 0,17 W/(m · K)), apresentando uma geometria semelhante à de uma superfície aletada, que são posteriormente empilhadas e fundidas para formarem o núcleo do trocador de calor. Além de ser barato, o trocador de calor pode ser facilmente reciclado ao final de sua vida útil. Dióxido de carbono, a uma temperatura média de 10°C e a uma pressão de 2 atm, escoa nos canais frios com uma velocidade média de um = 0,1 m/s. Ar, a 30°C e 2 atm, escoa nos canais quentes a 0,2 m/s. Desprezando a resistência térmica de contato na interface soldada, determine o produto do coeficiente de transferência de calor e da área de transferência de calor, UA, para um núcleo do trocador de calor constituído por 200 canais frios e 200 canais quentes.

Passo 1

Fala aí! Nosso enunciado pede o produto do coeficiente de transferência de calor e da área de transferência de calor...

Mas antes precisamos de uns dados adicionais que estão no apêndice do livro, tabela A-5, para o ar com T m ,   h = 303   K e p = 2   a t m :

k h = 0,0265   W / m . K c p ,   h = 1007   J / k g   .   K μ h = 186   .   10 - 7   N . s / m ²

P r h = 0,707 ρ h = 2,303   k g / m ³

E para o C O 2 com T m ,   c = 283   K :

k c = 0,0154   W / m . K c p ,   c = 833   J / k g   .   K μ c = 141   .   10 - 7   N . s / m ²

P r c = 0,765 ρ c = 3,76   k g / m ³

E para o propileno:

k p = 0,17   W / m . K

Passo 2

Agora precisamos fazer alguns cálculos antes de chegar no nosso objetivo, ok?

D h = 4   .   A c P

D h = 4   .   11   .   4 2   .   ( 11 + 4 )

D h = 5,87   m m

Agora podemos achar o número de Reynolds:

R e D ,   h = ρ h   .   u m ,   h   .   D h μ h R e D ,   c = ρ c   .   u m ,   c   .   D h μ c

R e D ,   h = 2,303   .   0,2   .   0,00587 186   .   10 - 7 R e D ,   c = 3,76   .   0,1   .   0,00587 141   .   10 - 7

R e D ,   h = 145 R e D ,   c = 156

Opa! Temos os dois fluxos laminares… Podemos então visitar a tabela 8.1 e assim encontramos um N u D = 3,82 , então vamos ter:

h h = N u D ,   h   .   k h D h h c = N u D ,   c   .   k c D c

h h = 3,82   .   0,0265 0,00587 h c = 3,82   .   0,0154 0,00587

h h = 17,2   W / m ² . K h c = 10   W / m ² . K

Passo 3

Podemos ver que nosso problema tem aletas estendendo-se para a direita e esquerda, nos dois tipos de fluidos. Por simetria, podemos ter:

L = d - c / 2

L = 5,5   m m

Estamos quase lá, falta pouco agora!

m h = h h   .   P k p   .   A c = 2   .   h h k p   .   b m c = 2   .   h c k p   .   b

m h = 2   .   17,2 0,17   .   0,004 m c = 2   .   10 0,17   .   0,004

m h = 225   m - 1 m c = 171,5   m - 1

Agora podemos encontrar o η f ,   h e o η f ,   c :

η f ,   h = t a n h m h   .   L m h   .   L η f ,   c = t a n h m c   .   L m c   .   L

η f ,   h = t a n h 225   .   0,0055 225   .   0,0055 η f ,   c = t a n h 171,5   .   0,0055 171,5   .   0,0055

η f ,   h = 0,682 η f ,   c = 0,781

E os η o ,   h e η o ,   c :

η o ,   h = 1 - A f A   .   1 - η f ,   h η o ,   c = 1 - A f A   .   1 - η f ,   c

η o ,   h = 1 - 2   .   L 2   .   L   +   a   .   1 - η f ,   h η o ,   c = 1 - 2   .   L 2   .   L   +   a   .   1 - η f ,   c

η o ,   h = 1 - 0,733   .   1 - 0,682 η o ,   c = 1 - 0,733   .   1 - 0,781

η o ,   h = 0,767 η o ,   c = 0,839

Passo 4

Beleza! Agora com um N = 200 e um w = 1 , assumindo que:

A = 2   .   L .   w   .   N = 3   .   w A w = ( a + b )   .   w   .   N = 1,6   .   w

A = 3   m ² A w = 1,6   m ²

Finalmente podemos chegar no grand finale!

1 U A = 1 η o ,   c   .   h c   .   A + c k p   .   A w + 1 η o ,   h   .   h h   .   A

1 U A = 1 0,839   .   10   .   3 + 0,004 0,17   .   1,6 + 1 0,767   .   17,2   .   3

U A = 12,6   W / m ² . K

Aeeee! Conseguimos! Um pouquinho complicada essa, mas juntos conseguimos resolver!

Resposta

U A = 12,6   W / m ² . K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O condensador de uma grande termoelétrica deve retirar 125 MW de calor de vapor condensado a 30°C h f g = 2431 k J k g . O resfriamento deve ser por água de resfriamento c p = 4180 J k g K de um rio p
Um aquecedor de casco e tubo deve ser selecionado para aquecer a água c p = 4190 J k g K de 20°C a 90°C com vapor escoando no lado do casco. A taxa de transferência de calor do aquecedor é de 600 kW.
Ar c p = 1005 J k g . K deve ser preaquecida por gases quentes em um trocador de calor de escoamento cruzado antes de sua entrada em um forno. O ar entra no trocador de calor a 95 kPa e 20°C, a uma ta
Em uma indústria químicas, determinado produto químico é aquecido por água quente fornecida por um forno de gás natural. A água quente c p = 4180 J k g K é então descarregada a 60°C a uma taxa de 8 k
O vapor saturado de água a 40 ℃ ℃ deve ser condensado ao escoar através do tubo de ar em um condensador resfriado a ar, a uma taxa de 0,2k g / s .O condensado deixa os tubos como um líquido saturado a