Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 38
Uma parede plana unidimensional, com espessura L, é construída com um material sólido com uma distribuição linear e não uniforme de porosidade, descrita por ). Represente graficamente as distribuições de temperaturas, em regime estacionário, , para , ; e , utilizando a expressão para a condutividade térmica efetiva mínima de um meio poroso, a expressão para a condutividade térmica efetiva máxima de um meio poroso, expressão de Maxwell, e para o caso no qual .
Passo 1
Beleza galerinha, vamos lá! A lei de Fourier pode ser expressa como:
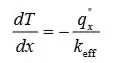
Observamos que o fluxo de calor é constante. A condutividade térmica efectiva pode ser avaliada a partir das várias fórmulas, como se segue.
Passo 2
Máxima condutividade térmica efectiva:
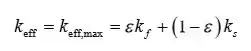
Condutividade térmica mínima efectiva:
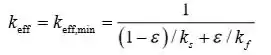
A expressão de Maxwell:
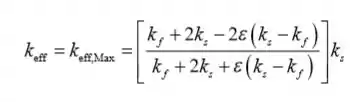
Passo 3
As Equações anteriores ser substituídas pela Equação 1 e a expressão pode ser integrada numericamente usando um código comercial. O IHT foi utilizado para gerar as seguintes distribuições de temperatura.
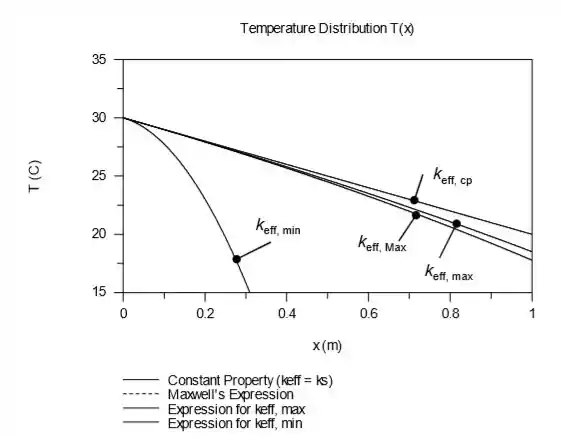
Resposta
Ei, a resposta está no passo a passo :)