Uma parede plana, que tem um de seus lados termicamente isolado, está inicialmente a uma temperatura uniforme , quando sua superfície exposta em tem a sua temperatura subitamente elevada para .
(a) Verifique se a equação a seguir satisfaz à equação do calor e às condições de contorno:
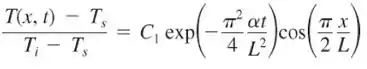
na qual é uma constante e é a difusividade térmica.
(b) Obtenha expressões para o fluxo térmico em e .
(c) Esboce a distribuição de temperaturas em , em , e em um instante de tempo intermediário. Esboce a variação com o tempo do fluxo térmico em , .
(d) Qual o efeito de na resposta térmica do material a uma mudança na temperatura de sua superfície?
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional sem geração de energia, logo a troca de calor só ocorre em uma direção que no caso apresentado é a radial, vamos fazer nosso diagrama pra facilitar nossa vida.
Origem e sentido da geração de calor e da dissipação.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Tendo tudo isso em mente vamos a nossa letra (a), que deseja verificar se a equação dada se adequa as condições de contorno, assim vamos escrever nossa lei de Fourier (equação ).

Como nossa condução é unidimensional e não há geração de energia, temos:
Substituindo pela equação apresentada no problema temos:
Aplicando nossas condições de contorno, temos:
Como todas as condições foram atendidas a nossa equação dada satisfaz nossas condições de contorno!
Passo 3
(b) Usando a equação da nossa primeira condição de contorno em (a), temos:
Passo 4
(c) Seguindo as equações da letra (a) e (b) vamos montar nosso gráfico , assim temos.

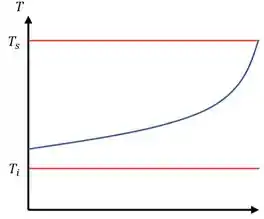
Passo 5
(d) Para encontrarmos o efeito de para uma mudança térmica temos que fazer uma relação com nossas temperaturas, assim temos:
Se , a temperatura tende para tende a chegar mais rápido em a mesma coisa para .
E é isso!
Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)