Uma peça de aço cujo teor inicial de carbono é de 0,10% em peso deve ser endurecida em um forno a 1150 K, por exposição a um gás de carburante. O coeficiente de difusão do carbono em aço é fortemente depende da temperatura, e na temperatura do forno é . Além disso, a fração de massa de carbono na superfície exposta da peça de aço é mantida em 0,011 pelo ambiente rico em carbono no forno. Considerando que o processo de endurecimento deve continuar até que a fração mássica de carbono a uma profundidade de 0,6 mm seja aumentada para 0,32%, determine quanto tempo a peça deve ser mantida no forno.
Passo 1
Bora continuar?
Então galera, o que temos aqui?
Nós temos as frações mássicas da espécie A em questão, certo? Temos que achar o tempo necessário para atingir a fração mássica a uma dada profundidade. Sendo assim, nós podemos usar uma fórmula que vai nos ajudar demaaais:
E o que sabemos?
Nooossa!! Olha que legal! Nós já temos tudo o que precisamos, então é só substituir:
Passo 2
Para achar a função erfc vamos ter que interpolar galera!
Olhem nossa tabelinha aí:
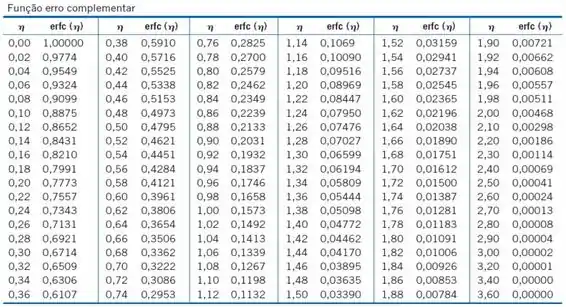
Como
Se lembram da interpolação?
Substituindo:
Se é assim:
E em horas:
E finalizamos mais umaa!!