Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 86

O perfil de velocidade no escoamento laminar completamente desenvolvido em um tubo circular, em m / s , é dado por u r = 4 1 - 100 r 2 , onde r é a distância radial a partir da linha central do tubo em m . Determine a o raio do tubo, b a velocidade média através do tubo e c a velocidade máxima no tubo.

Passo 1

Dados fornecidos:

Perfil de velocidade de um sistema totalmente desenvolvido

u r = 4 1 - 100 r 2

A distância radial do centro do tubo é  r .

Figura mostrando o perfil de velocidade:

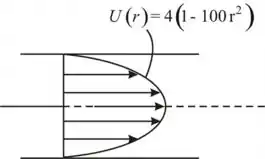
Passo 2

c) O enunciado forneceu o seguinte perfil de velocidade:

u r = 4 1 - 100 r 2

Temos que a velocidade é máxima na linha central de um tubo circular, ou seja, quando r = 0 .

Substituindo equação do perfil de velocidade temos:

V m á x = 4 1 - 100 × 0 2

V m á x = 4 1 - 0

V m á x = 4   m / s

Portanto, a velocidade máxima é  4   m / s

Passo 3

b) A velocidade média do fluxo é dada por

V m é d i a = V m á x 2

V m é d i a = 4   m / s 2

V m é d i a = 2   m / s

Portanto, a velocidade média é  2   m / s .

Passo 4

a) É importante saber que o perfil de velocidade de um fluxo laminar totalmente desenvolvido pode ser dado da seguinte maneira:

U r = V m á x 1 - r 2 R 2

O enunciado forneceu o seguinte perfil de velocidade:

u r = 4 1 - 100 r 2

Podemos comparando os dois perfis de velocidade da seguinte maneira:

4 1 - r 2 R 2 = 4 1 - 100 r 2

1 - r 2 R 2 = 1 - 100 r 2

r 2 R 2 = 100 r 2

1 R 2 = 100

R = 0,1   m

Portanto, o raio do tubo é  0,1   m .

Resposta

a) R = 0,1   m

b) V m é d i a = 2   m / s

c) V m á x = 4   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as condições do Problema 8.70, qual deve ser o comprimento da região anular se a vazão da água for de 0,35k g / s ao invés dos 0,02k g / s ?
Um gás ideal escoa no interior de um tubo de pequeno diâmetro. Deduza uma expressão para a densidade (massa específica) de transição do gás,ρ c , abaixo da qual os efeitos de microescala têm que ser l
Considere uma região anular entre dois tubos concêntricos na qual os diâmetros interno e externo são de 25m m e 50m m . Água entra na região anular a 0,0 3k g / s e 25 ° C . Se a parede do tubo intern
Ar, a 4 × 10 – 4k g / s e 20° C , entra em um duto retangular que tem 1m de comprimento e 4m m por 16m m de lado. Um fluxo térmico uniforme de 500W / m 2 é imposto na superfície do duto. Qual é a temp
Óleo a 150 ° C escoa lentamente através de um tubo longo com parede delgada e diâmetro interno de 3 5m m . O tubo está suspenso em uma sala na qual a temperatura do ar é de 2 5 ° C e o coeficiente de