Uma casa construída sobre a beira de um rio deve ser resfriada no verão com a utilização da água fria do rio que escoa a uma temperatura média de . Uma seção de de comprimento de um tubo circular de de diâmetro passa através da água. O ar entra a na seção do tubo submersa com velocidade de . Considerando que a superfície do duto esteja na temperatura da água determine a temperatura de saída do ar à medida que deixa a parte submersa do duto. Além disso, para um ventilador com eficiência global de , determine a potência do ventilador necessária para superar a resistência do escoamento na seção do duto.
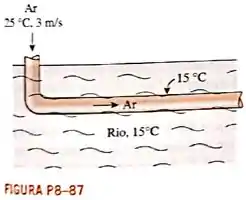
Passo 1
Dados fornecidos:
Diâmetro do tubo:
Comprimento do tubo:
Temperatura média da água:
Velocidade média do ar:
Eficiência geral do ventilador:
A temperatura inicial do ar que entra no duto:
Passo 2
Podemos obter as propriedades do ar na tabela A-15 a .
Densidade:
Calor específico:
Condutividade térmica:
Viscosidade cinemática:
Viscosidade dinâmica:
Número Prandtl:
Passo 3
Agora vamos calcular o número de Reynolds. Fazemos isso utilizando a seguinte relação:
Aqui, é a viscosidade cinemática, é a velocidade média e é o diâmetro do tubo. Substituindo os termos pelos dados fornecidos e calculados, temos:
Como o número de Reynolds é superior a 10.000, o fluxo é turbulento.
Temos que os comprimentos de entrada podem ser dados da seguinte maneira:
O comprimento da entrada é menor que o comprimento total do fluxo.
Passo 4
Podemos usar a relação de Dittus-Boelter para obter o número de Nusselt. Assim temos:
Substituindo os termos da equação pelos dados fornecidos, temos:
Com o número de Nusselt, podemos calcular o coeficiente de transferência de calor por convecção da seguinte maneira:
Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 5
Podemos obter a seguinte relação para fluxo volumétrico de ar:
Aqui, é a área da seção transversal.
Com o fluxo volumétrico, podemos obter uma relação para o fluxo mássico de ar. Assim temos:
Podemos obter uma relação para a área da superfície do tubo da seguinte maneira:
Agora, podemos então calcular a temperatura de saída usando a seguinte relação:
Aqui é a temperatura do fluxo de entrada, é a temperatura da superfície do tubo, é a temperatura do fluxo de saída, é a área da superfície, o coeficiente de transferência de calor e é a vazão mássica. Substituindo as relações encontradas temos:
Substituindo os termos pelos dados encontrados anteriormente e fornecidos no enunciado, temos:
Portanto, a temperatura de saída é .
Passo 6
Podemos calcular o fator de atrito para calcular as perdas de pressão. Pela equação de Petukhou, tubos lisos para o fator de atrito é dado pela seguinte equação:
Substituindo o número de Reynolds na equação, temos:
A perda de pressão no tubo pode ser dada pela seguinte relação:
Substituindo os termos da equação pelos dados fornecidos, temos:
O trabalho realizado pelo ventilador pode ser dado da seguinte forma:
Substituindo os termos da equação pelos dados fornecidos, temos:
Temos que a eficiência do ventilador pode ser calculada da seguinte forma:
Assim, a potência necessária para o ventilador é
Substituindo os termos da equação, temos:
Portanto, a entrada de energia necessária para superar a resistência ao fluxo na seção do duto é .