Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 93
Gases quentes saindo a de um motor disel estacionário entram em um tubo de de diâmetro com velocidade média de . A temperatura na superfície do tubo é . Determine o comprimento do tubo considerando que os gases de escape devem sair do tubo a após a transferência de calor para água na unidade de recuperação de calor. Use as propriedades do ar para os gases de escape.
Passo 1
Dados fornecidos:
Diâmetro do tubo:
Temperatura de entrada de gás:
Temperatura de saída do gás:
Temperatura da superfície do tubo:
Velocidade média de entrada:
Passo 2
Um diagrama esquemático do fluxo no tubo é o seguinte:
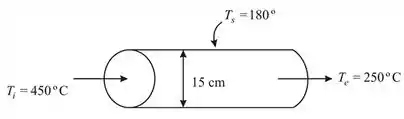
Passo 3
Precisamos calcular a temperatura média de filme para o ar com a seguinte relação:
Aqui, é a temperatura média de entrada e é a temperatura média de saída. Substituindo os termos pelos dados fornecidos no enunciado, temos:
Com o valor da temperatura média, podemos obter as seguintes propriedades para o ar a .
Densidade:
Condutividade térmica:
Viscosidade cinemática:
Calor específico:
Número e Prandtl:
Passo 4
Vamos começar calculando o número de Reynolds. Assim temos:
Substituindo os termos da equação pelos dados fornecidos, temos:
Como o número de Reynolds é maior que , temos que o fluxo é turbulento.
Passo 5
Aqui, vamos assumir que o fluxo é turbulento e totalmente desenvolvido. Assim, pela equação de Dittus – Boelter, podemos calcular o Número Nusselt. Assim temos:
Substituindo os termos da relação pelos dados fornecidos, temos:
Passo 6
Com o número de Nusselt, podemos calcular o coeficiente de transferência de calor usando a seguinte relação:
Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 7
Agora, vamos calcular a temperatura média logarítmica. Assim temos:
Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 8
Temos que a área superficial do tubo pode ser dada da seguinte maneia:
Podemos calcular a transferência de calor no tubo da seguinte maneira:
Substituindo a área superficial, temos:
Assim a transferência de calor por metro de comprimento do tubo é:
Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 9
Agora, podemos calcular a transferência de calor total no tubo pela expressão:
Onde a vazão mássica é e . Substituindo na equação acima, temos:
Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 10
Portanto, podemos calcular o comprimento do tubo da seguinte maneira:
Como a transferência de calor tem que ser a mesma , temos que:
Portanto, o comprimento do tubo é .