Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 99
Petróleo bruto a entra em um tubo de de diâmetro com velocidade média de . A temperatura média da parede do tubo é . As propriedades do petróleo bruto são as indicadas a seguir. Calcule a taxa de transferência de calor e o comprimento do tubo considerando que a temperatura de saída do petróleo bruto é .
Passo 1
Podemos desenhe o diagrama esquemático do fluxo do tubo da seguinte maneira:
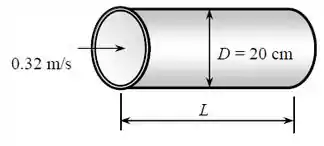
Hipóteses:
1) Existem condições de fluxo estáveis.
2) A temperatura da superfície é constante e uniforme.
3) As superfícies internas dos tubos são lisas.
4) A transferência de calor para os arredores é insignificante.
Passo 2
Dados fornecidos:
Diâmetro do tubo:
Temperatura de entrada do petróleo bruto:
Temperatura de saída do petróleo bruto:
Temperatura da parede do tubo:
Velocidade média de entrada:
Propriedades do petróleo:
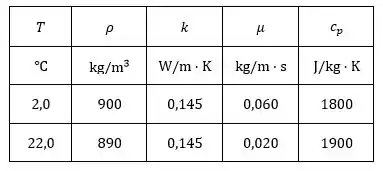
Passo 3
Vamos começar calculando a temperatura média. Assim temos:
Usando o método de interpolação podemos encontra as propriedades no óleo da temperatura média de . Assim temos:
Densidade:
Condutividade térmica:
Viscosidade dinâmica:
Calor específico:
Passo 4
Podemos calcular a taxa de transferência de calor usando a seguinte equação:
Aqui, é taxa de fluxo de massa , é o calor específico, é a temperatura de saída, é a temperatura de entrada
Onde é a área da seção transversal do tubo .
Substituindo os termos da equação pelos dados obtidos, temos:
Portanto a taxa de transferência de calor é .
Passo 5
Com os dados obtidos, vamos calcular o Número de Reynolds usando a seguinte expressão:
Substituindo os termos da equação pelos dados obtidos, temos:
Como o número de Reynolds está mais próximo de do que de , vamos assumir que o fluxo laminar totalmente desenvolvido.
Como nenhuma temperatura constante da superfície é fornecida, não podemos tirar o valor do número Nusselt da tabela.
Para encontrar Nusselt, primeiro vamos calcular o número de Prandtl usando a seguinte expressão:
Substituindo os termos da equação pelos dados obtidos, temos:
Passo 6
Podemos calcular o número de Nusselt pela equação de Edwards. Assim temos:
Substituindo os termos da equação pelos dados obtidos, temos:
O número de pode ser escrito da seguinte forma:
Rescrevendo isolando o coeficiente de transferência de calor por convecção, temos:
Substituindo os termos da equação pelos dados obtidos temos:
Passo 7
Podemos determinar o comprimento do tubo a partir de um balanço energético onde a taxa de transferência de calor calcular anteriormente é igual a:
Aqui, é o coeficiente de transferência de calor por convecção, é a temperatura média da superfície do tubo, é a média da temperatura de entrada e saída , e é a área da superfície do tubo . Assim temos:
Substituindo os termos da equação pelos dados obtidos temos:
Usando uma calculadora HP ou outra de sua preferência, encontramos que o comprimento do tubo é:
Portanto, o comprimento do tubo é .