Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 85

Uma placa de bronze quente está sendo resfriada na superfície superior por jato de ar a temperatura de 15   ° C e coeficiente de transferência de calor por convecção de   220 W m 2 ∙ K . A placa de bronze de 0   c m de espessura ρ = 8.530 k g m 3 ,   c p = 380 J k g ∙ K ,   k = 110 W m ∙ K ,   e   α = 33,9   10 6 m 2 s   tinha temperatura uniforme inicial de 650   ° C e a superfície inferior isolada. Utilizando espaçamento nodal uniforme ∆ x = 2,5   c m   e passo de tempo de ∆ t = 10   s , determine ( a ) equações implícitas de diferenças finitas e ( b ) temperaturas nodais da placa de bronze após 10 segundos de resfriamento.

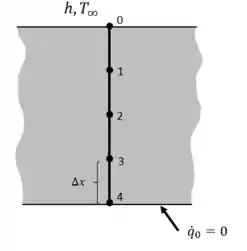
Passo 1

Bom, a partir do enunciado temos os seguintes dados:

∆ x = 2,5   c m ;   = 8.530 k g m 3 , ;   c p = 380 J k g ∙ K ;     k = 110 W m ∙ K ; h = 220 W m 2 ∙ K

  α = 33,9   10 6 m 2 s ; T ∞ = 15 ° C ;   ∆ t = 10   s    

Note que a superfície inferior se encontra isolada, logo os nós 1, 2, 3 e 4 podem ser tratados como nós interiores, o que significa que podemos utilizar a expressão abaixo;

τ T m - 1 i + 1 - 1 + 2 τ T m i + 1 + τ T m + 1 i + 1 + T m i = 0

Para o nó 0, onde é nó de contorno e temos a presença de convecção, aplicando o balanço de energia...

- 1 + 2 τ + 2 h ∆ x k τ T 0 i + 1 + 2 τ T 1 i + 1 + T 0 + 2 h ∆ x k τ T ∞ = 0

Passo 2

Aplicando a formulação nos restantes dos nós temos:

N ó   0 :

- 1 + 2 τ + 2 h ∆ x k τ T 0 i + 1 + 2 τ T 1 i + 1 + T 0 + 2 h ∆ x k τ T ∞ = 0

N ó   1 :

τ T 0 i + 1 - 1 + 2 τ T 1 i + 1 + τ T 2 i + 1 + T 1 i = 0    

N ó   2 :

τ T 1 i + 1 - 1 + 2 τ T 2 i + 1 + τ T 3 i + 1 + T 2 i = 0    

N ó   3 :

τ T 2 i + 1 - 1 + 2 τ T 3 i + 1 + τ T 4 i + 1 + T 3 i = 0    

N ó   4 :

τ T 3 i + 1 - 1 + 2 τ T 4 i + 1 + τ T 3 i + 1 + T 4 i = 0    

Onde para o termo τ ...

τ = σ ∆ t ∆ x 2 = 33,9 × 10 - 6 m 2 s 10   s 0,025   m 2 = 0,5424

Resposta

Resolvendo as equações simultaneamente temos as seguintes temperaturas:

T 0 = 631,2 ° C

T 1 = 644,7 ° C

T 2 = 648,5 ° C

T 3 = 649,6 ° C

T 4 = 649,8 ° C

Ver Outros Exercícios desse livro