Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 39
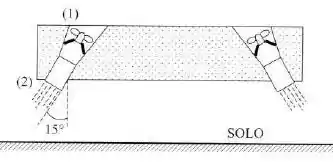
Uma plataforma de cargas é sustentada por quatro jatos de ar inclinados, para favorecer a estabilidade e as manobras. Admite-se que, na entrada e na saída, a pressão seja atmosférica e igual a e a temperatura seja . Admite-se que na entrada a área seja muito grande e na saída o diâmetro seja de . A plataforma é dimensionada para sustentar, em repouso, um total de .
- Qual a mínima vazão em massa que deve ser produzida por cada ventilador?
- Qual a mínima potência do motor de cada ventilador, se o seu rendimento é e a perda de carga ao longo dos condutos é desprezível?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos calcular a força que cada ventilador deve gerar para sustentar uma carga de . Como a plataforma tem quatro ventiladores inclinados em um ângulo de , podemos escrever a força de um ventilador como:
A velocidade de saída do gás é dada por:
Como:
Temos que:
A densidade do ar é dada por:
Portanto:
Passo 2
Vamos calcular agora a potência mínima de cada ventilador da seguinte forma:
Como:
Temos que:
A potência mínima de cada ventilador será: