Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 6
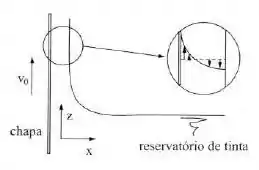
Uma chapa fina deve passar de forma contínua num banho de tinta contido num reservatório, como mostra a figura. Em regime permanente, o diagrama de velocidades bidimensional é tal que, numa seção, a vazão é nula, já que parte da tinta sobe arrastada pela chapa e retorna por gravidade, mantendo a espessura constante. Como a velocidade da chapa é baixa, admite-se que o atrito com o ar é desprezível. Determinar:
- a expressão do diagrama de velocidades;
- a velocidade de subida da chapa para que a espessura da camada de tinta seja .
Dados: ; .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Como o movimento do fluido obedece a um regime permanente, temos que:
Em que é função somente de .
Assim, utilizando as equações fornecidas na seção , temos que:
Como a espessura não varia, consequentemente a pressão não irá variar ao longo de , ou seja:
Portanto, teremos que:
Passo 2
Integrando duas vezes ambos os lados da equação acima, temos:
E:
Resolvendo, temos que:
Passo 3
A constante será a velocidade do fluido na superfície da chapa, ou seja, . Fazendo , temos que:
Isso implica que a constante será:
Dessa forma, substituindo os valores das constantes encontradas, temos que a expressão do diagrama de velocidades será dada por:
Passo 4
Para o item b, temos que:
Como a vazão é nula numa seção da chapa, temos que:
Desenvolvendo a equação, temos que:
Logo:
Substituindo os dados conhecidos, temos que:
Ou: