A potência, , necessária para acionar uma hélice depende das seguintes variáveis: velocidade da corrente livre, , diâmetro da hélice, , velocidade angular, , viscosidade do fluido, , massa específica do fluido, , e velocidade do som no fluido, . Quantos grupos adimensionais são necessários para caracterizar esta situação? Obtenha estes grupos adimensionais.
Passo 1
Nessa questão nós temos a relação funcional entre o poder de acionar uma hélice marítima e outros parâmetros físicos. Com isso, queremos encontrar o número de termos que caracterizam esse fenômeno e os termos
Passo 2
Usando o procedimento de Buckingham temos que o número de parâmetros é:
![]()
Selecionando as dimensões primárias :
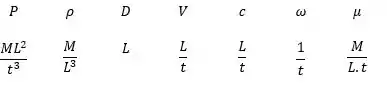
E os parâmetros repetidos:
![]()
Passo 3
Então nós temos grupos sem dimensão. Configurando as equações dimensionais:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 4
Para o segundo grupo temos:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 5
Para o terceiro grupo temos:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 6
Para o quarto grupo temos:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 7
Verificando usando as dimensões :