A taxa à qual a temperatura no centro de um grão de arroz diminui durante um processo de tecnologia de alimentos é crítica — um valor muito alto leva à quebra do grão e um valor muito baixo torna o processo lento e caro. A taxa depende do calor específico, , da condutividade térmica, , e do tamanho, , do grão de arroz, bem como do calor específico, , da massa específica, , da viscosidade, , e da velocidade, , do ar de resfriamento. Quantas dimensões básicas estão incluídas nestas variáveis? Determine os parâmetros para este problema.

Usando o procedimento de Buckingham temos que o número de parâmetros é:

Selecionando as dimensões primárias (temperatura):

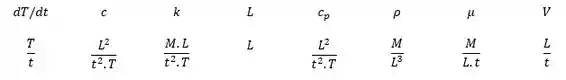
E os parâmetros repetidos:

Então nós temos grupos sem dimensão. Por inspeção, um grupo é e configurando as equações dimensionais:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Por um processo semelhante ao passo anterior, encontramos:

E,

Então,