Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 14.Problemas - Ex. 13
A presença de uma pequena quantidade de ar pode causar uma redução significativa na taxa de transferência de calor na superfície de um condensador de vapor de água que é resfriada com água. Para uma superfície limpa, com vapor de água puro e as condições especificadas, a taxa de condensação é de Com a presença de ar estagnado no vapor, a temperatura da superfície do condensado cai de para , e a taxa de condensação é reduzida pela metade.
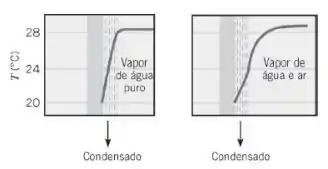
Para a mistura ar–vapor de água, determine a pressão parcial do ar como uma função da distância do filme de condensado.
Passo 1
Nessa questão nós temos que a superfície limpa com vapor puro possui a taxa de condensação de para as condições dadas. Com a presença de ar estagnado no vapor, a superfície do condensado cai de para e a taxa de condensação é reduzida pela metade.
Com essas informações vamos encontrar a pressão parcial do ar na mistura ar-vapor em função da distância do filme de condensado.
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições em estado estacionário;
(2) Propriedades constantes, incluindo pressão na mistura ar-vapor;
(3) Comportamento perfeito dos gases.
A distribuição parcial da pressão do ar em função da distância pode ser encontrada a partir da expressão da taxa de espécies
Passo 3
Com,
E,
Reconhecendo que,
Encontramos,
Passo 4
Com,
Com em e em onde , a temperatura média da mistura ar-vapor, e
Os valores selecionados para a pressão são mostrados abaixo e a distribuição é mostrada acima:
Resposta
